题目内容
19.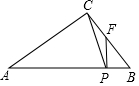 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,点P为边AB上的一个动点,过点P作AB的垂线交BC所在的直线于点F,连接CP,当△CFP为等腰三角形时,求PF的长.
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,点P为边AB上的一个动点,过点P作AB的垂线交BC所在的直线于点F,连接CP,当△CFP为等腰三角形时,求PF的长.
分析 由勾股定理求出AB,证得△PBF∽CBA;分两种情况讨论:
①当PF=CF时,根据三角形相似的性质,列出方程,解方程即可;
②当PC=CF时,根据三角形相似的性质,列出方程,解方程即可.
解答  解:∵∠ACB=90°,AC=8,BC=6,
解:∵∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵PF⊥AB,
∴∠BPF=90°,
∴∠ACB=∠BPF,
∵∠ABC=∠FBP,
∴△PBF∽CBA,
∴$\frac{PF}{AC}$=$\frac{BF}{AB}$,
分两种情况讨论:
①当PF=CF时,如图1,
设PF=x,则CF=x,BF=6-x,
∴$\frac{x}{8}$=$\frac{6-x}{10}$,
解得x=$\frac{8}{3}$
②当PC=CF时,则∠F=∠CPF,
∴∠B=∠CPB,
∴PC=BC=6,如图2,
,设PF=x,则BF=12,
∴$\frac{x}{8}$=$\frac{12}{10}$
解得x=$\frac{48}{5}$;
综上所述:当△PCF为等腰三角形时,PF的长为:$\frac{8}{3}$或$\frac{48}{5}$.
点评 本题考查了等腰三角形的性质;本题有一定难度,需要进行分类讨论.

练习册系列答案
相关题目
10. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,且AF=2,则点F到边DC的距离为( )
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,且AF=2,则点F到边DC的距离为( )
 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,且AF=2,则点F到边DC的距离为( )
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,且AF=2,则点F到边DC的距离为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
 如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,△DEF是什么三角形?说明理由.
如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,△DEF是什么三角形?说明理由. 如图,已知$\widehat{AB}$=$\widehat{CD}$,试说明AD=CB.
如图,已知$\widehat{AB}$=$\widehat{CD}$,试说明AD=CB. 矩形ABCD中,M是AD的中点,N是BC的中点,点P是CD的延长线连接PM延长交AC于点Q,连接PN,QN.
矩形ABCD中,M是AD的中点,N是BC的中点,点P是CD的延长线连接PM延长交AC于点Q,连接PN,QN.