题目内容
9. 如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,△DEF是什么三角形?说明理由.
如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,△DEF是什么三角形?说明理由.
分析 根据AB=AC,D是BC中点,DE⊥AB于E,DF⊥AC于F,利用角角边定理可证此题;
解答 证明:∵AB=AC,D是BC中点,
∴∠ABC=∠ACB,BD=DC.
∵DE⊥AB于E,DF⊥AC于F,
∴∠DEB=∠DFC=90°
在△DEB和△DFC中,
$\left\{\begin{array}{l}{∠DEB=∠DFC}\\{∠ABC=∠ACB}\\{BD=DC}\end{array}\right.$,
∴△DEB≌△DFC(AAS),
∴DE=DF,
∴∠DEF=∠DFE;
∴△DEF是等腰三角形.
点评 此题主要考查学生对全等三角形的判定与性质和等腰三角形的性质的理解和掌握,难度不大,是一道基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
19.已知⊙O的半径为r,圆心到点A的距离为d,且r,d分别是方程x2-4x+3=0的两根,则点A与⊙O的位置关系是 (( )
| A. | 点A在⊙O内部 | B. | 点A在⊙O上 | C. | 点A在⊙O外部 | D. | 点A不在⊙O上 |
 已知平面直角坐标系xOy,已知二次函数y=x2-2bx+3的图象过x轴上点A(3,0),且与y轴交于点B,顶点为点P.
已知平面直角坐标系xOy,已知二次函数y=x2-2bx+3的图象过x轴上点A(3,0),且与y轴交于点B,顶点为点P.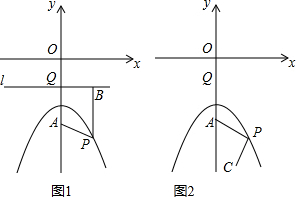
 如图,圆锥底面半径为r cm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为6cm.
如图,圆锥底面半径为r cm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为6cm.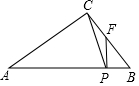 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,点P为边AB上的一个动点,过点P作AB的垂线交BC所在的直线于点F,连接CP,当△CFP为等腰三角形时,求PF的长.
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,点P为边AB上的一个动点,过点P作AB的垂线交BC所在的直线于点F,连接CP,当△CFP为等腰三角形时,求PF的长.