题目内容
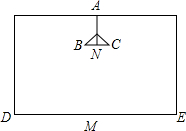 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8m,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,
在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8m,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,| 2 |
考点:中心投影,相似三角形的应用
专题:应用题
分析:根据题意画出几何图,则AN=0.08m,AM=2m,计算出DE=4
m,再证明△ABC∽△ADB,然后利用相似比可计算出BC.
| 2 |
解答:解:如图,光线恰好照在墙角D、E处 ,AN=0.08m,AM=2m,
,AN=0.08m,AM=2m,
由于房间的地面为边长为4m的正方形,则DE=4
m,
∵BC∥DE,
∴△ABC∽△ADB,
∴
=
,即
=
,
∴BC≈0.23(m).
答:灯罩的直径BC约为0.23m.
 ,AN=0.08m,AM=2m,
,AN=0.08m,AM=2m,由于房间的地面为边长为4m的正方形,则DE=4
| 2 |
∵BC∥DE,
∴△ABC∽△ADB,
∴
| BC |
| DE |
| AN |
| AM |
| BC | ||
4
|
| 0.08 |
| 2 |
∴BC≈0.23(m).
答:灯罩的直径BC约为0.23m.
点评:本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.合理使用相似的知识解决有关计算,计算时注意单位要统一.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
对于函数y=4x2,下列说法正确的是( )
| A、当x>0时,y随x的增大而减小 |
| B、当x<0时,y随x的增大而减小 |
| C、y随x的增大而减小 |
| D、y随x的增大而增大 |
 如图,在等腰梯形ABCD中,AD∥BC,AB=3,∠B=60°,DE∥AB,则CE等于
如图,在等腰梯形ABCD中,AD∥BC,AB=3,∠B=60°,DE∥AB,则CE等于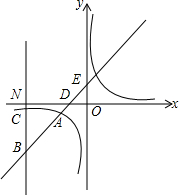 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y= “健康、快乐、向上”立方体纸盒表面展开图如图,则与印有“健”字面相对的表面上印有
“健康、快乐、向上”立方体纸盒表面展开图如图,则与印有“健”字面相对的表面上印有