题目内容
3．已知实数x、y满足$\sqrt{2x-1}$+（y+2）2=0，那么xy的值为（ ）| A． | -$\frac{1}{4}$ | B． | $\frac{1}{4}$ | C． | -4 | D． | 4 |
分析 首先利用二次根式以及偶次方的性质得出x，y的值，进而利用负指数幂的性质得出答案．
解答 解：∵$\sqrt{2x-1}$+（y+2）2=0，
∴2x-1=0，y+2=0，
解得：x=$\frac{1}{2}$，y=-2，
故xy=（$\frac{1}{2}$）-2=4．
故选：D．
点评 此题主要考查了二次根式以及偶次方的性质，正确得出x，y的值是解题关键．
练习册系列答案
相关题目
13．已知3x=4y，则$\frac{x}{y}$的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{7}$ | D． | $\frac{4}{7}$ |
14．甲地到乙地之间的铁路长210千米，动车运行后的平均速度是原来火车的1.6倍，这样由甲地到乙地的行驶时间缩短了1.5小时，设原来火车的平均速度为x千米/小时，则下列方程正确的是（ ）
| A． | $\frac{210}{x}$-1.5=$\frac{210}{1.6x}$ | B． | $\frac{210}{x}$+1.6=$\frac{210}{1.5x}$ | ||
| C． | $\frac{210}{x}$+1.5=$\frac{210}{1.6x}$ | D． | $\frac{210}{x}$-1.6=$\frac{210}{1.5x}$ |
18．解方程$\frac{3x+2}{4}$-$\frac{5x+1}{12}$=1-$\frac{2x-1}{2}$时，去分母正确的是（ ）
| A． | 3（3x+2）-5x+1=12-6（2x-1） | B． | 3（3x+2）-5x-1=1-6（2x-1） | ||
| C． | 3（3x+2）-5x-1=12-6（2x-1） | D． | （3x+2）-5x+1=12-6（2x-1） |
8．
如图，AB∥CD，∠E=37°，∠C=20°，则∠EAB=（ ）
如图，AB∥CD，∠E=37°，∠C=20°，则∠EAB=（ ）| A． | 37° | B． | 20° | C． | 17° | D． | 57° |
15．九年级一班有七个学习小组，每组人数如下：5，5，6，x，6，7，8，已知平均每个小组有6个，则这组数据的众数与中位数分别是（ ）
| A． | 5，6 | B． | 6，5 | C． | 6，7 | D． | 5，8 |
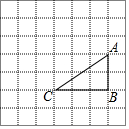如图，在边长为1的正方形网格中，△ABC的顶点均在格点上，点A、B的坐标分别是A（4，3）、B（4，1），把△ABC绕点C逆时针旋转90°后得到△A1B1C．则A1的坐标为（-1，4）．