题目内容
19.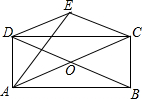 如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.
如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.(1)求证:四边形OCED是菱形;
(2)连接AE,若AB=6cm,BC=$\sqrt{5}$cm.
①求sin∠EAD的值;
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.
分析 (1)只要证明四边相等即可证明;
(2)①设AE交CD于K.由DE∥AC,DE=OC=OA,推出$\frac{DK}{KC}$=$\frac{DE}{AC}$=$\frac{1}{2}$,由AB=CD=6,可得DK=2,CK=4,在Rt△ADK中,AK=$\sqrt{A{D}^{2}+D{K}^{2}}$=$\sqrt{(\sqrt{5})^{2}+{2}^{2}}$=3,根据sin∠DAE=$\frac{DK}{AK}$计算即可解决问题;
②作PF⊥AD于F.易知PF=AP•sin∠DAE=$\frac{2}{3}$AP,因为点Q的运动时间t=$\frac{OP}{1}$+$\frac{AP}{\frac{3}{2}}$=OP+$\frac{2}{3}$AP=OP+PF,所以当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,由此即可解决问题.
解答 (1)证明:∵四边形ABCD是矩形.
∴OD=OB=OC=OA,
∵△EDC和△ODC关于CD对称,
∴DE=DO,CE=CO,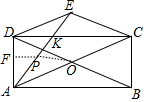
∴DE=EC=CO=OD,
∴四边形CODE是菱形.
(2)①设AE交CD于K.
∵四边形CODE是菱形,
∴DE∥AC,DE=OC=OA,
∴$\frac{DK}{KC}$=$\frac{DE}{AC}$=$\frac{1}{2}$
∵AB=CD=6,
∴DK=2,CK=4,
在Rt△ADK中,AK=$\sqrt{A{D}^{2}+D{K}^{2}}$=$\sqrt{(\sqrt{5})^{2}+{2}^{2}}$=3,
∴sin∠DAE=$\frac{DK}{AK}$=$\frac{2}{3}$,
②作PF⊥AD于F.易知PF=AP•sin∠DAE=$\frac{2}{3}$AP,
∵点Q的运动时间t=$\frac{OP}{1}$+$\frac{AP}{\frac{3}{2}}$=OP+$\frac{2}{3}$AP=OP+PF,
∴当O、P、F共线时,OP+PF的值最小,此时OF是△ACD的中位线,
∴OF=$\frac{1}{2}$CD=3.AF=$\frac{1}{2}$AD=$\frac{\sqrt{5}}{2}$,PF=$\frac{1}{2}$DK=1,
∴AP=$\sqrt{(\frac{\sqrt{5}}{2})^{2}+{1}^{2}}$=$\frac{3}{2}$,
∴当点Q沿上述路线运动到点A所需要的时间最短时,AP的长为$\frac{3}{2}$,点Q走完全程所需的时间为3s.
点评 本题考查四边形综合题、矩形的性质、菱形的判定和性质、锐角三角函数、平行线分线段成比例定理、勾股定理、三角形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用垂线段最短解决最值问题,所以中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. | 0.826×106 | B. | 8.26×107 | C. | 82.6×106 | D. | 8.26×108 |
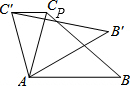 如图,在△ABC中,∠CAB=78°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与B′C′交于点P,则∠BPB′的大小为24°.
如图,在△ABC中,∠CAB=78°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与B′C′交于点P,则∠BPB′的大小为24°. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.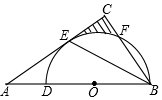 如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
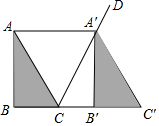 如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.
如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.