题目内容
8.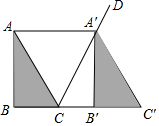 如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.
如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.(1)判断四边形ACC'A'的形状,并说明理由;
(2)在△ABC中,∠B=90°,A B=24,cos∠BAC=$\frac{12}{13}$,求CB'的长.
分析 (1)根据平行四边形的判定定理(有一组对边平行且相等的四边形是平四边形)推知四边形ACC'A'是平行四边形.又对角线平分对角的平行四边形是菱形推知四边形ACC'A'是菱形.
(2)通过解直角△ABC得到AC、BC的长度,由(1)中菱形ACC'A'的性质推知AC=AA′,由平移的性质得到四边形ABB′A′是平行四边形,则AA′=BB′,所以CB′=BB′-BC.
解答  解:(1)四边形ACC'A'是菱形.理由如下:
解:(1)四边形ACC'A'是菱形.理由如下:
由平移的性质得到:AC∥A′C′,且AC=A′C′,
则四边形ACC'A'是平行四边形.
∴∠ACC′=∠AA′C′,
又∵CD平分∠ACB的外角,即CD平分∠ACC′,
∴CD也平分∠AA′C′,
∴四边形ACC'A'是菱形.
(2)∵在△ABC中,∠B=90°,AB=24,cos∠BAC=$\frac{12}{13}$,
∴cos∠BAC=$\frac{AB}{AC}$=$\frac{12}{13}$,即$\frac{24}{AC}$=$\frac{12}{13}$,
∴AC=26.
∴由勾股定理知:BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{2{6}^{2}-2{4}^{2}}$=10.
又由(1)知,四边形ACC'A'是菱形,
∴AC=AA′=26.
由平移的性质得到:AB∥A′B′,AB=A′B′,则四边形ABB′A′是平行四边形,
∴AA′=BB′=26,
∴CB′=BB′-BC=26-10=16.
点评 本题考查了四边形综合题,需要掌握平移的性质,解直角三角形,勾股定理以及菱形的判定与性质等知识点.解答(1)题时,往往误认为四边形ACC'A'是平行四边形,岂不知还要根据已知条件继续证得该四边形是菱形,属于易错题.

练习册系列答案
相关题目
16.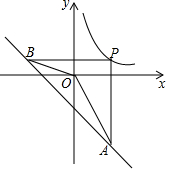 如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )
如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )
 如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )
如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
13.太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为( )
| A. | 1.5×108 | B. | 1.5×109 | C. | 0.15×109 | D. | 15×107 |
20.铁路部门消息:2017年“端午节”小长假期间,全国铁路客流量达到4640万人次,4640万用科学记数法表示为( )
| A. | 4.64×105 | B. | 4.64×106 | C. | 4.64×107 | D. | 4.64×108 |
17.在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动.为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
关于这组数据,下列说法正确的是( )
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 4 | 12 | 16 | 17 | 1 |
| A. | 中位数是2 | B. | 众数是17 | C. | 平均数是2 | D. | 方差是2 |
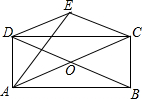 如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.
如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.