题目内容

9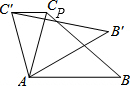．如图，在△ABC中，∠CAB=78°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，BC与B′C′交于点P，则∠BPB′的大小为24°．

分析 旋转中心为点A，B与B′，C与C′分别是对应点，根据旋转的性质可知，旋转角∠BAB′=∠CAC′，AC=AC′，再利用平行线的性质得∠C′CA=∠CAB，把问题转化到等腰△ACC′中，根据内角和定理求∠CAC′，即可求出∠BAB′的度数，然后根据三角形的内角和即可得到结论．

解答 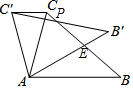解：∵CC′∥AB，∠CAB=78°，
∴∠C′CA=∠CAB=78°，
又∵C、C′为对应点，点A为旋转中心，
∴AC=AC′，即△ACC′为等腰三角形，
∴∠BAB′=∠CAC′=180°-2∠C′CA=24°，
∵∠AEB=∠B′EP，∠B=∠B′，
∴∠BPB′=∠BAB′=24°，
故答案为：24°．

点评 本题考查了旋转的基本性质，对应点到旋转中心的距离相等，对应点与旋转中心的连线的夹角为旋转角．同时考查了平行线的性质．

练习册系列答案
相关题目
12．计算或化简：
（1）-22+（π-2017）0-2sin60°+|1-$\sqrt{3}}$|；       
（2）a（3-2a）+2（a+1）（a-1）．
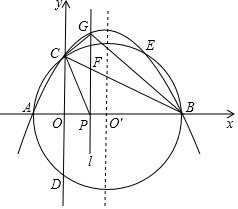20．如图，在平面直角坐标系中，已知A（-2，0），C（0，4），点O′为x轴上一点，⊙O′过A，C两点交x轴于另一点B．
（1）求点O′的坐标；
（2）已知抛物线y=ax2+bx+c过A，B，C三点，且与⊙O′交于另一点E，求抛物线的解析式，并直接写出点E 坐标；
（3）设点P（t，0）是线段OB上一个动点，过点P作直线l⊥x轴，交线段BC于F，交抛物线y=ax2+bx+c于点G，请用t表示四边形BPCG的面积S；
（4）在（3）的条件下，四边形BPCG能否为平行四边形？若能，请求出t的值；若不能，请说明理由．
17．在平面直角坐标系中，点A的坐标是（-2，3），作点A关于x轴的对称点，得到点A′，再将点A'向右平移3个单位得到点A″，则点A''的坐标是（1，-3）．
4．（1）计算：（3-π）0-$\sqrt{9}$+|3-$\sqrt{3}$|+（tan30°）-1
（2）定义新运算：对于任意实数a，b，都有a⊕b=a（a-b）+1，等式右边是通常的加法、减法及乘法运算．
比如：2⊕5=2×（2-5）+1
=2×（-3）+1
=-6+1
=-5
若3⊕x的值小于13，求x的取值范围，并在如图所示的数轴上表示出来．
14．如图所示的几何体由一个圆柱体和一个长方体组成，它的主视图是（　　）
A．B．C．D．
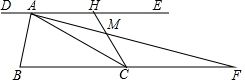1．如图，过锐角△ABC的顶点A作DE∥BC，AB恰好平分∠DAC，AF平分∠EAC交BC的延长线于点F．在AF上取点M，使得AM=$\frac{1}{3}$AF，连接CM并延长交直线DE于点H．若AC=2，△AMH的面积是$\frac{1}{12}$，则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$．
18．定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠BCP=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点．
请你运用所学知识，结合上述材料，解决下列问题：
在平面直角坐标系中，点M是曲线y=$\frac{3\sqrt{3}}{x}$（x＞0）上的任意一点，点N是x轴正半轴上的任意一点．
（1）如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（$\sqrt{3}$，3），点N的坐标是（$\sqrt{3}$，0）时，求点P的坐标；
（2）如图3，当点M的坐标是（3，$\sqrt{3}$），点N的坐标是（2，0）时，求△MON的自相似点的坐标；
（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由．
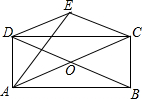19．如图，矩形ABCD的对角线AC，BD相交于点O，△COD关于CD的对称图形为△CED．
（1）求证：四边形OCED是菱形；
（2）连接AE，若AB=6cm，BC=$\sqrt{5}$cm．
①求sin∠EAD的值；
②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1.5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网