题目内容
15.阅读课本材料,解答后面的问题.折纸与证明
折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(图1),怎样证明∠C>∠B呢?
把AC沿∠A的平分线AD翻折,因为AB>AC,所以,点C落在AB上的点C′处(图2).于是,由∠AC′D>∠B,可得∠C>∠B.
在△ABC中,∠B=2∠C,点D为线段BC上一动点,当AD满足某种条件时,探讨在线段AB、BD、CD、AC四条线段中,某两条或某三条线段之间存在的数量关系.
(1)如图3,当AD⊥BC时,求证:AB+BD=DC;
(2)如图4,当AD是∠BAC的角平分线时,写出AB、BD、AC的数量关系,并证明.

分析 (1)在DC上截取DE=BD,连接AE,证明CE=AB即可;
(2)在AC上截取AF=AB,连接DF,证明CF=BD即可;
解答 解:(1)如图3,在DC上截取DE=BD,连接AE,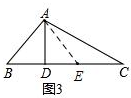
∵AD⊥BC,
∴AB=AE,∠ABD=∠AED,
∵∠ABD=2∠C,
∴∠AED=2∠C,
∵∠AED=∠C+∠EAC,
∴∠C=∠EAC,
∴EC=AE=AB,
∴CD=DE+EC=AB+BD;
(2)AB+BD=AC.
如图4,在AC上截取AF=AB,连接DF,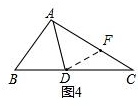
∵AD是∠BAC的角平分线,
∴∠BAD=∠FAD,
在△ABD和△AFD中
$\left\{\begin{array}{l}{AB=AF}\\{∠BAD=∠FAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AFD(SAS),
∴∠AFD=∠B=2∠C,BD=DF,
∵∠AFD=∠C+∠FDC,
∴∠FDC=∠C,
∴FC=FD=BD,
∴AC=AF+FC=AB+BD.
点评 本题考查了等腰三角形的性质、角平分线的性质、全等三角形的判定与性质等知识点,难度适中.在证明线段和差关系等式时,往往采用截长补短法,截长就是将长的那条线段一分为二,并让其中一条等于两条短线段当中的一条,这样就只需证明剩下的两条线段对应相等即可;补短就是将两条短线段拼接在一起形一条长线段,然后只需证明两条长线段相等即可.截长补短体现的是“分”与“合”的不同思维,但最终的效果是一致的.

练习册系列答案
相关题目
6.小明的座位在第5排第4列,简记为(5,4),张扬的座位在第3排第2列,简记为(3,2),若小伟的座位在小明的后面相距2排,同时在他的左边相距3列,则小伟的座位可简记为( )
| A. | (2,7) | B. | (7,1) | C. | (8,2) | D. | (6,5) |
4.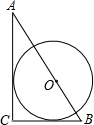 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )| A. | $\frac{24}{7}$ | B. | 4 | C. | 5 | D. | 2 |
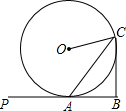 如图,AB为⊙O的切线,A为切点,点C在⊙O上,BC⊥PB于点 B,OC为⊙O的半径.
如图,AB为⊙O的切线,A为切点,点C在⊙O上,BC⊥PB于点 B,OC为⊙O的半径.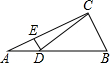 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,D是AB边上的一个动点(不与点A,B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示与的函数关系的图象大致是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,D是AB边上的一个动点(不与点A,B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示与的函数关系的图象大致是( )