题目内容
甲、乙两人同时从环形跑道上同一点出发,沿顺时针方向跑步,甲的速度比乙快,过一段时间,甲第一次从背后追上乙,这时甲立即背转方向,以原来的速度沿逆时针方向跑去,当两人再次相遇时,乙恰好跑了四圈,求甲的速度是乙的几倍?
考点:多元一次方程组
专题:应用题
分析:设环形跑道周长为a,甲的速度为x,乙的速度为y,根据甲、乙两人两次相遇时所用的时间相等建立等量关系,然后将方程恒等变形后解方程就可解决问题.
解答:解:设环形跑道周长为a,甲的速度为x,乙的速度为y,
根据题意可得:
+
=
,
∵a>0,
∴
+
=
,
去分母并整理得:2x2-xy-2y2=0,
∵y>0,
∴2•(
)2-
-2=0,
解得:
=
或
=
(舍负).
答:甲的速度是乙的
倍.
根据题意可得:
| a |
| x-y |
| a |
| x+y |
| 4a |
| y |
∵a>0,
∴
| 1 |
| x-y |
| 1 |
| x+y |
| 4 |
| y |
去分母并整理得:2x2-xy-2y2=0,
∵y>0,
∴2•(
| x |
| y |
| x |
| y |
解得:
| x |
| y |
1+
| ||
| 4 |
| x |
| y |
1-
| ||
| 4 |
答:甲的速度是乙的
1+
| ||
| 4 |
点评:本题考查的是有关环形跑道的问题,解决本题的关键是设中间元(设环形跑道周长为a),根据甲、乙两人两次相遇时所用的时间相等建立等量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
n个连续自然数按规律排列如下:

根据规律,2005所在位置为( )

根据规律,2005所在位置为( )
| A、第1002列,第1行 |
| B、第1002列,第2行 |
| C、第1003列,第1行 |
| D、第1003列,第2行 |
 如图,已知a∥b,直线c与a,b相交,若∠1=60°,则∠2=
如图,已知a∥b,直线c与a,b相交,若∠1=60°,则∠2= 如图,AD是△ABC的BC边上的中线,AB=7,AD=5,则AC的取值范围为
如图,AD是△ABC的BC边上的中线,AB=7,AD=5,则AC的取值范围为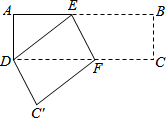 在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=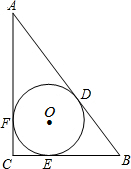 如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O的半径长为3cm,AC=10cm,则AD长度为
如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O的半径长为3cm,AC=10cm,则AD长度为