题目内容
1.任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个),求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数的和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32,它们的和是154.三位数223各个数位上的数的和是7,154÷7=22.再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.分析 举例三位数为578与123,找出所有可能的两位数,求出之和,除以各位数字得到结果,归纳总结得到一般性结论,验证即可.
解答 解:举例1:三位数578:$\frac{57+75+78+87+58+85}{5+7+8}$=22;
举例2:三位数123:$\frac{12+21+13+31+23+32}{1+2+3}$=22,(任意举两个三位数进行探究,得出正确结论均可)
猜想:所有可能的两位数的和除以这几个数字的和恒等于22,
证明如下:设三位数为100a+10b+c(a,b,c≠0),
所有的两位数是10a+b,10a+c,10b+a,10b+c,10c+a,10c+b,
则有$\frac{10a+b+10b+a+10a+c+10c+a+10b+c+10c+b}{a+b+c}$=$\frac{22(a+b+c)}{a+b+c}$=22.
点评 此题考查了整式的加减,以及列代数式,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
9.根据表中一次函数的自变量与它的对应值表
可得P的值为1.
| x | -2 | 0 | 1 |
| y | 3 | P | 0 |
10.用配方法解一元二次方程x2+2x-5=0,此方程可变形为( )
| A. | (x-1)2=6 | B. | (x+1)2=6 | C. | (x+1)2=4 | D. | (x-1)2=1 |
11.下列说法中,正确的是( )
| A. | $\sqrt{25}$=±5 | B. | $\sqrt{6}$是6的一个平方根 | ||
| C. | 8的立方根是±2 | D. | -32的算术平方根是3 |
 -3mx+6m=0的一个根,则m的值为( )
-3mx+6m=0的一个根,则m的值为( ) 根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为21.
根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为21.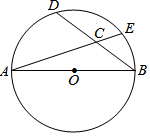 如图,AB是⊙O的直径,点D是弧AE的中点,AB=5,BD=4,则sin∠ECB=$\frac{4}{5}$.
如图,AB是⊙O的直径,点D是弧AE的中点,AB=5,BD=4,则sin∠ECB=$\frac{4}{5}$.