题目内容
7. 如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,求证:EF=DF.
如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,求证:EF=DF.
分析 根据AAS推出△ABD≌△CBE,根据全等三角形的性质得出AB=BC,求出AE=CD,根据AAS推出△AEF≌△CDF,得出对应边相等即可.
解答 证明:在△ABD和△CBE中,$\left\{\begin{array}{l}{∠BAD=∠BCE}&{\;}\\{∠B=∠B}&{\;}\\{BD=BE}&{\;}\end{array}\right.$,
∴△ABD≌△CBE(AAS),
∴AB=BC,
∵BE=BD,
∴AE=CD,
在△AEF和△CDF中,$\left\{\begin{array}{l}{∠AFE=∠CFD}&{\;}\\{∠EAF=∠DCF}&{\;}\\{AE=CD}&{\;}\end{array}\right.$,
∴△AEF≌△CDF(AAS),
∴EF=DF.
点评 本题考查了全等三角形的判定与性质;本题难度适中,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.在进行异号的两个有理数加法运算时,用到下面的一些操作:
①将绝对值较大的有理数的符号作为结果的符号并记住
②将记住的符号和绝对值的差一起作为最终的计算结果
③用较大的绝对值减去较小的绝对值
④求两个有理数的绝对值
⑤比较两个绝对值的大小
其中操作顺序正确的步骤是( )
①将绝对值较大的有理数的符号作为结果的符号并记住
②将记住的符号和绝对值的差一起作为最终的计算结果
③用较大的绝对值减去较小的绝对值
④求两个有理数的绝对值
⑤比较两个绝对值的大小
其中操作顺序正确的步骤是( )
| A. | ①②③④⑤ | B. | ④⑤③②① | C. | ①⑤③④② | D. | ④⑤①③② |
19.某县教育局为了解某校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表

(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中生人数.
某校初中生阅读数学教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |

(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中生人数.
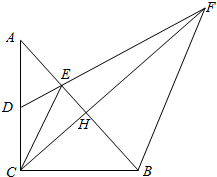 如图,在△ABC中,∠ACB=90°,CH⊥AB,H为垂足,D是AC的中点,CE平分∠ACH交AB于E,DE与CH的延长线交于点F,求证:BF∥CE.
如图,在△ABC中,∠ACB=90°,CH⊥AB,H为垂足,D是AC的中点,CE平分∠ACH交AB于E,DE与CH的延长线交于点F,求证:BF∥CE.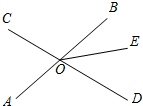 如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.
如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.