题目内容
11．下列命题是假命题的是（ ）| A． | 如果m∥n，n∥l，那么m∥l （m、n、l为三条不重合的直线） | |
| B． | 三角形中至少有一个角大于或等于60° | |
| C． | 平行四边形的对角线相交且互相平分 | |
| D． | 两条直线被第三条直线所截，同位角相等 |
分析 根据平行公理、三角形内角和定理、平行四边形的性质、平行线的性质判断即可．
解答 解：如果m∥n，n∥l，那么m∥l （m、n、l为三条不重合的直线）是真命题；
三角形中至少有一个角大于或等于60°是真命题；
平行四边形的对角线相交且互相平分是真命题；
两条直线被第三条直线所截，同位角相等，缺少平行的条件，是假命题，
故选：D．
点评 主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
2．做重复试验：抛掷一枚啤酒瓶盖1000次．经过统计得“凸面向上”的次数为420次，则可以由此估计抛掷这枚啤酒瓶盖出现“凸面向上”的概率约为（ ）
| A． | 0.22 | B． | 0.42 | C． | 0.50 | D． | 0.58 |
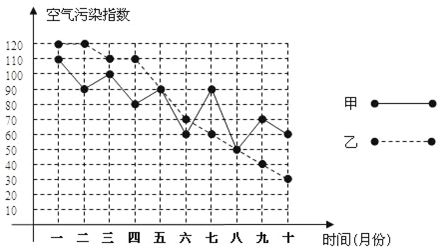
19．甲、乙两城市为了解决空气质量污染问题，对城市及其周边的环境污染进行了综合治理．在治理的过程中，环保部门每月初对两城市的空气质量进行监测，连续10个月的空气污染指数如图所示．其中，空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．
（1）填写下表：
（2）从以下四个方面对甲、乙两城市的空气质量进行分析．
①从平均数和空气质量为优的次数来分析：空气质量为优的次数甲城市比乙城市少；（填“多”或“少），乙城市的空气质量比甲城市的空气质量好些．（填“好些”或“差些”）；
②从平均数和中位数来分析：甲的中位数＜乙的中位数（填“=”、“＞”或“＜”），空气质量相对较好的城市是乙（填“甲”或“乙”）；
③从平均数和方差来分析：S甲2＜S乙2，空气污染指数比较稳定的城市是甲（填“甲”或“乙”）；
④根据折线图上两城市的空气污染指数的走势来分析，两城市治理环境污染的效果较好的城市是乙（填“甲”或“乙”）．
（1）填写下表：
| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 1 | |
| 乙 | 1060 | 80 | 3 |
①从平均数和空气质量为优的次数来分析：空气质量为优的次数甲城市比乙城市少；（填“多”或“少），乙城市的空气质量比甲城市的空气质量好些．（填“好些”或“差些”）；
②从平均数和中位数来分析：甲的中位数＜乙的中位数（填“=”、“＞”或“＜”），空气质量相对较好的城市是乙（填“甲”或“乙”）；
③从平均数和方差来分析：S甲2＜S乙2，空气污染指数比较稳定的城市是甲（填“甲”或“乙”）；
④根据折线图上两城市的空气污染指数的走势来分析，两城市治理环境污染的效果较好的城市是乙（填“甲”或“乙”）．
6．下列计算正确的是（ ）
| A． | a6÷a3=a2 | B． | （a3）2=a5 | C． | （ab）3=ab3 | D． | a•a2=a3 |
