题目内容
6.已知方程x2-3x+k=0有一个根是-1,则该方程的另一根是( )| A. | 1 | B. | 0 | C. | -4 | D. | 4 |
分析 根据根与系数的关系可得:方程两根之和为3,两根之积为k,将其中一根代入求解即可.
解答 解:设另外一个根为x,则x+(-1)=3,
解得:x=4.
故选D.
点评 本题考查了根与系数的关系,解答本题的关键是掌握两根之和为-$\frac{b}{a}$.

练习册系列答案
相关题目
16.在以下实数:-$\sqrt{2}$,$\sqrt{16}$,π,3.1416,($\sqrt{3}$)2,$\frac{22}{7}$,0.15,0.020020002…(每两个2之间零的个数依次增加1)中,无理数有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元; 乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
按上述优惠条件,若贝贝第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品各多少件?
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
1.下列从左到右的变形中,属于因式分解的是( )
| A. | (x+y)(x-2y)=x2-xy+y2 | B. | 3x2-x=x(3x-1) | ||
| C. | (a-b)2=(a-b)(a-b) | D. | m2-n2=(m-n)2 |
11.顺次连结对角线垂直的四边形各边中点,所得四边形是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 任意四边形 |
16.一元二次方程x2+3=2$\sqrt{3}$x的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的有理根 | ||
| C. | 有两个相等的无理根 | D. | 没有实数根 |
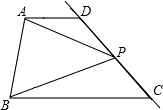 如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).
如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).