题目内容
9. 如图,在等腰梯形ABCD中,AB∥CD,点E在对角线AC上,且∠1=∠2,AB=5,BC=AD=$\sqrt{10}$,CD=3.
如图,在等腰梯形ABCD中,AB∥CD,点E在对角线AC上,且∠1=∠2,AB=5,BC=AD=$\sqrt{10}$,CD=3.(1)求证:△CDE∽△ABC;
(2)求:$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值.
分析 (1)由AB∥CD,得到∠ACD=∠CAB,根据已知条件∠1=∠2,于是得到结论;
(2)根据相似三角形的性质得到$\frac{{S}_{△CDE}}{{S}_{△ABC}}$=($\frac{CD}{AB}$)2=$\frac{9}{25}$,由CD∥AB,于是得到△ACD与△ABC的高相等.求得$\frac{{S}_{△ACD}}{{S}_{△ABC}}$=$\frac{CD}{AB}$=$\frac{3}{5}$=$\frac{15}{25}$,即可得到结论.
解答 解:(1)∵AB∥CD,
∴∠ACD=∠CAB,
∵∠1=∠2,
∴△CDE∽△ABC;
(2)∵△CDE∽△ABC,
∴$\frac{{S}_{△CDE}}{{S}_{△ABC}}$=($\frac{CD}{AB}$)2=$\frac{9}{25}$,
∵CD∥AB,
∴△ACD与△ABC的高相等.
∴$\frac{{S}_{△ACD}}{{S}_{△ABC}}$=$\frac{CD}{AB}$=$\frac{3}{5}$=$\frac{15}{25}$,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{{S}_{△ADE}-{S}_{△CDE}}{{S}_{△ABC}}$=$\frac{6}{25}$.
点评 本题考查了相似三角形的判定和性质,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1.⊙O内一点M到圆的最大距离为10cm,最短距离为8cm,那么过M点的最短弦长为( )
| A. | 1cm | B. | 8$\sqrt{5}$cm | C. | $\sqrt{41}$cm | D. | 9cm |
 ___________
___________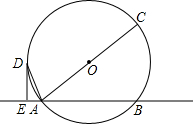 如图,直线EF交⊙O于A,B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
如图,直线EF交⊙O于A,B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
 按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,第2013次得到的结果为3.
按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,第2013次得到的结果为3. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)