题目内容
15.化简$\sqrt{\frac{2R{h}_{1}}{2R{h}_{2}}}$的结果是( )| A. | $\sqrt{\frac{{h}_{1}}{{h}_{2}}}$ | B. | $\frac{\sqrt{{h}_{1}}}{\sqrt{{h}_{2}}}$ | C. | $\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{2}}$ | D. | $\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{1}}$ |
分析 根据二次根式的性质进行化简,即可解答.
解答 解:$\sqrt{\frac{2R{h}_{1}}{2R{h}_{2}}}$=$\sqrt{\frac{{h}_{1}}{{h}_{2}}}$=.$\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{2}}$
故选:C.
点评 本题考查了二次根式的性质,解决本题的关键是熟记二次根式的性质.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.已知在一次函数y=-2x+b的图象上有三点(-2,y1),(-1,y2)(1,y3),则y1,y2,y3的大小关系( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y2>y1 | D. | y3>y1>y2 |
3.用中位数去估计总体时,其优越性是( )
| A. | 运算简便 | B. | 不受个别数据较大或较小的影响 | ||
| C. | 不受较小数据的影响 | D. | 不受较大数据的影响 |
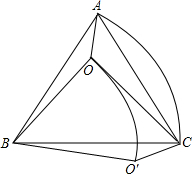 如图,O是等边△ABC中一点,OA=2,OB=3,∠AOB=150°,∠BOC=115°,将△AOB绕点B顺时针旋转60°至△CO′B,下列说法中:
如图,O是等边△ABC中一点,OA=2,OB=3,∠AOB=150°,∠BOC=115°,将△AOB绕点B顺时针旋转60°至△CO′B,下列说法中: