题目内容
13.三角形的三边长分别是5cm,12cm,13cm,点P、Q分别为内心和外心,则PQ=$\frac{\sqrt{65}}{2}$.分析 如图△ABC中,AB=5,BC=12,AC=13,点P、Q分别为内心和外心,作PE⊥BC于E,PF⊥AC于F,PD⊥AB于D.在Rt△PQF中求出PF、FQ即可解决问题.
解答 解:如图△ABC中,AB=5,BC=12,AC=13,点P、Q分别为内心和外心,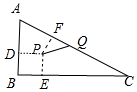
作PE⊥BC于E,PF⊥AC于F,PD⊥AB于D.
∵AB2+BC2=52+122=169,AC2=132=169,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∵PD=PE=PF,∠B=∠PDB=∠PEB=90°,
∴四边形PDBE是矩形,
∵PD=PE,
∴四边形PDBE是正方形,设边长为a,
∵$\frac{1}{2}$•BC•AB=$\frac{1}{2}$a•(AB+BC+AC),
∴$\frac{1}{2}$×5×12=$\frac{1}{2}$×a×30,
∴a=2,
∴AD=AF=5-2=3,
∵AQ=QC=6.5,
∴FQ=AQ-AF=3.5,
∴在Rt△PFQ中,PQ=$\sqrt{P{F}^{2}+F{Q}^{2}}$=$\sqrt{{2}^{2}+3.{5}^{2}}$=$\frac{\sqrt{65}}{2}$.
故答案为$\frac{\sqrt{65}}{2}$.
点评 本题考查三角形内切圆与内心、勾股定理以及逆定理、三角形的外接圆与圆心等知识,解题的关键是熟练应用这些知识解决问题,学会添加辅助线构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,∠BAC=90°,BC=5cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中阴影部分)的面积为2πcm2.
如图,在△ABC中,∠BAC=90°,BC=5cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中阴影部分)的面积为2πcm2.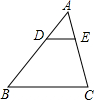 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{BD}$=$\frac{2}{3}$,DE=4,则BC的长为10.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{BD}$=$\frac{2}{3}$,DE=4,则BC的长为10. 如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是8.
如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是8.