题目内容
3．
如图，在△ABC中，∠BAC=90°，BC=5cm，AC=3cm，将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置，则线段AB扫过区域（图中阴影部分）的面积为2πcm2．
分析 根据阴影部分的面积是：S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1，分别求得：扇形BCB1的面积，S△CB1A1，S△ABC以及扇形CAA1的面积，即可求解．
解答 解：∵在△ABC中，∠BAC=90°，BC=5cm，AC=3cm，
∴AB=$\sqrt{B{C}^{2}-A{C}^{2}}$=4cm．
扇形BCB1的面积是=$\frac{45π×{5}^{2}}{360}$=$\frac{25π}{8}$，
S△CB1A1=$\frac{1}{2}$×3×4=6；
S扇形CAA1=$\frac{45π×{3}^{2}}{360}$=$\frac{9π}{8}$．
故S阴影部分=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1=$\frac{25π}{8}$+6-6-$\frac{9π}{8}$=2π．
故答案为：2π．
点评 本题考查了扇形的面积的计算，正确理解阴影部分的面积=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1是关键．
练习册系列答案
相关题目
13．顶点为（5，1），形状与函数y=$\frac{1}{3}$x2的图象相同且开口方向相反的抛物线是（ ）
| A． | y=-$\frac{1}{3}{（{x-5}）^2}$+1 | B． | y=-$\frac{1}{3}$x2-5 | C． | y=-$\frac{1}{3}$（x-5）2-1 | D． | y=$\frac{1}{3}$（x+5）2-1 |
如图，△ABC中，角平分线BO与CO的相交点O，OE∥AB，OF∥AC，BC=10，则△OEF的周长=10．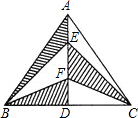
如图，在△ABC中，AB=AC，点D是BC中点，若BC=5，AD=4，则图中阴影部分的面积为5．