题目内容
9. 如图,已知在Rt△ABC中,AB=AC=$\frac{3\sqrt{2}}{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2016个内接正方形的边长为($\frac{1}{2}$)2015.
如图,已知在Rt△ABC中,AB=AC=$\frac{3\sqrt{2}}{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2016个内接正方形的边长为($\frac{1}{2}$)2015.
分析 先求出第一个、第二个、第三个正方形的边长,探究规律后即可解决问题.
解答  解:∵AB=AC=$\frac{3\sqrt{2}}{2}$,∠A=90°,
解:∵AB=AC=$\frac{3\sqrt{2}}{2}$,∠A=90°,
∴∠B=∠C=45°,BC=$\sqrt{2}$AC=3
∵四边形GDEF是正方形,
∴∠GDE=∠FED=90°,GF=GD=DE=EF,
∴∠BDG=∠CEF=90°,
∴∠B=∠BGD=45°,∠C=∠EFC=45°,
∴BD=DG=DE=EC=EF,
∴DE=$\frac{1}{3}$BC=1,
∴第一个正方形边长为1,设第二个正方形边长为x,
∵∠JDH=∠DPG,∠DGP=∠DHJ=90°,
∴△DGP∽△JHD,
∴$\frac{DG}{JH}$=$\frac{GP}{DH}$,
∴$\frac{1}{x}$=$\frac{\frac{1}{2}}{DH}$,
∴DH=$\frac{1}{2}$x,同理,IE=$\frac{1}{2}$x,
∵DE=DH+HI+IE,
∴1=2x,
∴x=$\frac{1}{2}$,
∴第二个正方形边长为$\frac{1}{2}$=($\frac{1}{2}$)1,同理第三个正方形边长为$\frac{1}{4}$=($\frac{1}{2}$)2,…,
∴第2016个内接正方形的边长为($\frac{1}{2}$)2015,
故答案为($\frac{1}{2}$)2015.
点评 本题考查正方形的性质.相似三角形的判定和性质、规律题型等知识,解题的关键是学会从特殊到一般,探究规律,利用规律解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.下列语句:
①任何数的零次方都等于1;
②如果两条直线被第三条直线所截,那么同位角相等;
③一个图形和它经过平移所得的图形中,两组对应点的连线平行且相等;
④平行线间的距离处处相等.
说法错误的有( )个.
①任何数的零次方都等于1;
②如果两条直线被第三条直线所截,那么同位角相等;
③一个图形和它经过平移所得的图形中,两组对应点的连线平行且相等;
④平行线间的距离处处相等.
说法错误的有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )| A. | 1元 | B. | 2元 | C. | 3元 | D. | 4元 |
4.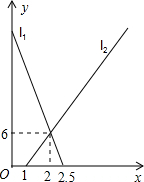 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )| A. | 12 km/h,3 km/h | B. | 15km/h,3km/h | C. | 12 km/h,6 km/h | D. | 15km/h,6km/h |
14.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a6÷a3=a2 | C. | 4x3-3x2=1 | D. | (-2x2y)3=-8x6y3 |
18.某班同学在探究弹簧长度跟外力的关系变化时,实验记录得到的数据如表:
则y关于x的函数图象是( )
| 砝码的质量(x克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 指针位置(y厘米) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 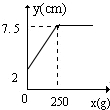 | B. | 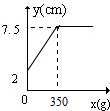 | C. | 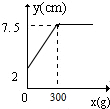 | D. |  |