题目内容
1.以下说法合理的是( )| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30% | |
| B. | 掷一枚骰子,掷出点6的概率是$\frac{1}{6}$,意思是每掷6次就有1次掷得点数为6 | |
| C. | 某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖 | |
| D. | 甲、乙两组同学分别进行抛掷硬币的试验,正面朝上的频率分别为0.48和0.51 |
分析 直接利用概率的意义分别分析得出答案.
解答 解:A、小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%,实验次数太少,没有代表性,故此选项错误;
B、掷一枚骰子,掷出点6的概率是$\frac{1}{6}$,意思是大量实验平均每掷6次就有1次掷得点数为6,故此选项错误;
C、某彩票的中奖机会是2%,那么买100张彩票一定会有2张中奖,错误,不一定有两张中奖;
D、甲、乙两组同学分别进行抛掷硬币的试验,正面朝上的频率分别为0.48和0.51,正确.
故选:D.
点评 此题主要考查了概率的意义,正确把握概率的意义是解题关键.

练习册系列答案
相关题目
16.下列各数中,无理数是( )
| A. | $\sqrt{36}$ | B. | $\sqrt{7}$ | C. | $\frac{22}{7}$ | D. | 3.141 |
6.过n边形的一个顶点画出所有的对角线,可以将这个n边形分成的三角形的个数是( )
| A. | n | B. | n-1 | C. | n-2 | D. | n-3 |
13.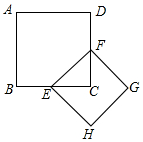 如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
 如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$+1 | D. | 2$\sqrt{2}$ |
10.若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
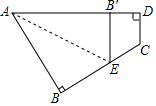 如图所示,一个四边形纸片ABCD,∠D=90°把纸片按如图所示折叠,使点B落在AD上的B′处,AE是折痕.
如图所示,一个四边形纸片ABCD,∠D=90°把纸片按如图所示折叠,使点B落在AD上的B′处,AE是折痕.