题目内容
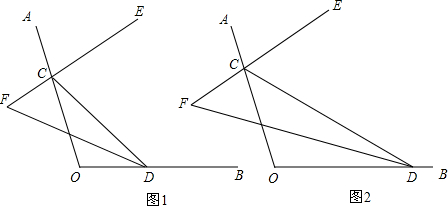
3.如图,∠AOB=110°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.(1)当∠OCD=30°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,写出求出∠F变化范围;若不变,请说明理由.
分析 (1)根据三角形的内角和是180°,可求∠CDO=40°,所以∠CDF=20°,又由平角定义,可求∠ACD=150°,所以∠ECD=75°,又根据三角形的外角等于与它不相邻的两内角之和,可求∠ECD=∠F+∠CDF,∠F=55°.
(2)同理可证,∠F=45度.
解答 解:(1)∵∠AOB=110°∠OCD=30°,
∴∠CDO=40°.
∵CE是∠ACD的平分线DF是∠CDO的平分线,
∴∠ECD=75°,∠CDF=20°.
∵∠ECD=∠F+∠CDF,
∴∠F=55°.
(2)不变化,∠F=55°.
∵∠AOB=110°,
∴∠CDO=110°-∠OCD,∠ACD=180°-∠OCD,
∵CE是∠ACD的平分线,DF是∠CDO的平分线,
∴∠ECD=110°-$\frac{1}{2}$∠OCD,∠CDF=55°-$\frac{1}{2}$∠OCD.
∵∠ECD=∠F+∠CDF,
∴∠F=55°.
点评 本题考查了三角形的外角等于与它不相邻的两内角之和,以及三角形的内角和是180°的定理.

练习册系列答案
相关题目
12.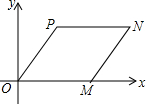 如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )
如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )
 如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )
如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )| A. | (7,4) | B. | (8,4) | C. | (9,4) | D. | (10,4) |
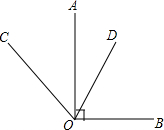 已知,如图,OA⊥BO于点O,OC是∠AOB外部一条射线,且∠AOC=40°,又OD平分∠COB,求∠AOD的度数.
已知,如图,OA⊥BO于点O,OC是∠AOB外部一条射线,且∠AOC=40°,又OD平分∠COB,求∠AOD的度数.