题目内容
12.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折弦,且∠APB<90°,Q是a,b之间且在折线APB左侧的一点,如图.
(1)若∠1=33°,∠APB=74°,则∠2=41度.
(2)若∠Q的一边与PA平行,另一边与PB平行,请探究∠Q,∠1,2间满足的数量关系并说明理由.
(3)若∠Q的一边与PA垂直,另一边与PB平行,请直接写出∠Q,∠1,2之间满足的数量关系.
分析 (1)图1,过P作PC∥直线a,根据平行线的性质得到∠1=∠APC,∠2=∠BPC,于是得到结论;
(2)如图2,由已知条件得到四边形MQNP是平行四边形,根据平行四边形的性质得到∠MQN=∠P=∠1+∠2,根据平角的定义即可得到结论;
(3)由垂直的定义得到∠QEP=90°,由平行线的性质得到∠QFE=∠P,根据平角的定义得到结论.
解答  解:(1)图1,过P作PC∥直线a,
解:(1)图1,过P作PC∥直线a,
∴PC∥b,
∴∠1=∠APC,∠2=∠BPC,
∴∠2=∠APB-∠1=41°;
故答案为:41;
(2)如图2,∵QM∥PB,QN∥PA,
∴四边形MQNP是平行四边形,
∴∠MQN=∠P=∠1+∠2,
∴∠EQN=180°-∠MQM=180°-∠1-∠2;
即∠Q=∠1+∠2或,∠Q=180°-∠1-∠2;
(3)∵QE⊥AP,
∴∠QEP=90°,
∵QF∥PB,
∴∠QFE=∠P,
∴∠EQF=90°-∠QFE=90°-∠1-∠2,
∴∠EQG=180°-∠EQF=90°+∠1+∠2.
点评 本题考查了平行线的性质,平行四边形的判定和性质,平角的定义,正确的作出图形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的角平分线BO、CO交于O点,过O点作DE∥BC,求出∠BOC的大小.
如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的角平分线BO、CO交于O点,过O点作DE∥BC,求出∠BOC的大小. 如图,△ABC内接于⊙O,OD⊥AC于D,OD=2,OC=4,则∠B=60°.
如图,△ABC内接于⊙O,OD⊥AC于D,OD=2,OC=4,则∠B=60°.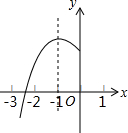 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论: