题目内容
20.从-2,-1,-$\frac{2}{3}$,0,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程$\frac{ax+2}{x-3}=1$的解为非负数,且满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$只有三个整数解的概率是$\frac{1}{6}$.分析 首先求得关于x的方程$\frac{ax+2}{x-3}=1$的解为非负数时a的值,满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解时a的值,再利用概率公式即可求得答案.
解答 解:∵关于x的方程$\frac{ax+2}{x-3}=1$的解为非负数,
∴x=$\frac{5}{1-a}$≥0,
∴1-a>0,
∴a=-2、-1、-$\frac{2}{3}$、0;
∵满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解,
即a<x≤2有三个整数解;
∴使得关于x的方程程$\frac{ax+2}{x-3}=1$的解为非负数,且满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解的有1个,
∴使得关于x的方程$\frac{ax+2}{x-3}=1$的解为非负数,且满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解的概率是:$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 此题考查了概率公式的应用、分式方程解的情况以及不等式组的解集.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要( )个小立方块.
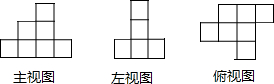

| A. | 36 | B. | 52 | C. | 54 | D. | 55 |
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 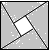 | B. |  | C. | 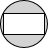 | D. | 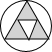 |
15.如果点K、L、M、N分别是四边形ABCD的四条边AB、BC、CD、DA的中点,且四边形KLMN是菱形,那么下列选项正确的是( )
| A. | AB⊥BC | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
5. 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
 老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )
老北京的老行当中有一行叫做“抓彩卖糖”:商贩将高丽纸裁成许多小条,用矾水在上面写上糖的块数,最少一块,多的是三块或五块,再将枝条混合在一起.游戏时叫儿童随意抽取一张,然后放入水罐中浸湿,即出现白道儿,按照上面的白道儿数给糖.一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块塘的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块塘的纸条的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
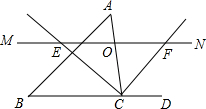 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.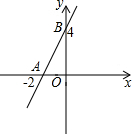 如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )
如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )

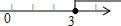
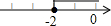
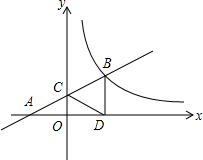 如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.
如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.