题目内容
 如图,在边长为3的正方形ABCD中,⊙O1与⊙O2外切,且⊙O1分别与DA、DC边相切,⊙O2分别与BA、BC边相切,则圆心距O1 O2为( )
如图,在边长为3的正方形ABCD中,⊙O1与⊙O2外切,且⊙O1分别与DA、DC边相切,⊙O2分别与BA、BC边相切,则圆心距O1 O2为( )A、6-3
| ||
| B、2.4 | ||
C、4-2
| ||
D、
|
考点:相切两圆的性质
专题:
分析:通过作辅助线构造直角三角形,用勾股定理作为相等关系列方程求解.
解答: 解:如图所示,过点O1作O1F⊥CD交CD于点F,过点O2作O2E⊥AB于点E.
解:如图所示,过点O1作O1F⊥CD交CD于点F,过点O2作O2E⊥AB于点E.
设⊙O1半径x,⊙O2半径y,
∵O1在∠ADC的平分线上;O2在∠ABC平分线上,而BD为正方形对角线,平分对角,
∴O1O2 在BD上,
∴∠ADB=∠DBA=45°,
∴DO1=
x,BO2=
y
则 DB=DO1+O1O2+O2B=x+y+
(x+y)=3
解得x+y=
=6-3
.
故选:A.
 解:如图所示,过点O1作O1F⊥CD交CD于点F,过点O2作O2E⊥AB于点E.
解:如图所示,过点O1作O1F⊥CD交CD于点F,过点O2作O2E⊥AB于点E.设⊙O1半径x,⊙O2半径y,
∵O1在∠ADC的平分线上;O2在∠ABC平分线上,而BD为正方形对角线,平分对角,
∴O1O2 在BD上,
∴∠ADB=∠DBA=45°,
∴DO1=
| 2 |
| 2 |
则 DB=DO1+O1O2+O2B=x+y+
| 2 |
| 2 |
解得x+y=
3
| ||
|
| 2 |
故选:A.
点评:此题主要考查了相切两圆中的有关计算问题.解题方法主要是利用正方形的性质构造直角三角形,用勾股定理作为相等关系列方程求解.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 如图,直线AB、CD相交于点O,OD平分∠BOE,OF平分∠AOE,则∠AOF的余角的个数为( )
如图,直线AB、CD相交于点O,OD平分∠BOE,OF平分∠AOE,则∠AOF的余角的个数为( )| A、1个 | B、2个 | C、3个 | D、4个 |
 已知△ABC中,AB=AC直线DF交AB于点D,交BC于点E,交AC的延长线于点F,BD=CF,求证:DE=EF.
已知△ABC中,AB=AC直线DF交AB于点D,交BC于点E,交AC的延长线于点F,BD=CF,求证:DE=EF. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,BD⊥CD,如果AD=1,BC=3,那么BD长是
如图,在梯形ABCD中,AD∥BC,AB⊥AD,BD⊥CD,如果AD=1,BC=3,那么BD长是 如图,观察海岛(AB),立两标杆(CD,EF),并使点F,D,B在同一直线上,两标杆前后相距1000步,标杆均高3丈,若从标杆CD后退123步,观察者的眼睛H(靠近地面)与标杆顶端C,岛的峰顶A在同一直线上;从标杆EF后退127步,同样观察者的眼睛K(靠近地面)与标杆顶端E,岛的峰顶A在同一直线上;问海岛的峰高AB和海岛离标杆CD的距离BD分别为多少?(注:1步=6尺,1丈=10尺)
如图,观察海岛(AB),立两标杆(CD,EF),并使点F,D,B在同一直线上,两标杆前后相距1000步,标杆均高3丈,若从标杆CD后退123步,观察者的眼睛H(靠近地面)与标杆顶端C,岛的峰顶A在同一直线上;从标杆EF后退127步,同样观察者的眼睛K(靠近地面)与标杆顶端E,岛的峰顶A在同一直线上;问海岛的峰高AB和海岛离标杆CD的距离BD分别为多少?(注:1步=6尺,1丈=10尺)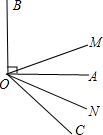 如图,已知∠AOB是直角,ON平分∠AOC,OM平分∠BOC,则∠MON=
如图,已知∠AOB是直角,ON平分∠AOC,OM平分∠BOC,则∠MON= 如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )


