题目内容
如果多项式(x2+mx+n)(x2-3x+4)展开后不含x3和x2项,则m,n的值分别是( )
| A、3,4 | B、4,3 |
| C、3,5 | D、5,3 |
考点:多项式乘多项式
专题:
分析:首先利用多项式乘以多项式的法则得出x2和x3项的系数,进而得出m,n的值.
解答:解:(x2+mx+n)(x2-3x+4)
=x4-3x3+4x2+mx3-3mx2+4mx+nx2-3nx+4n
=x4+(m-3)x3+(4-3m+n)x2+4mx-3nx+4n
∵不含x3和x2项,
∴m=3,n=5,
故选C.
=x4-3x3+4x2+mx3-3mx2+4mx+nx2-3nx+4n
=x4+(m-3)x3+(4-3m+n)x2+4mx-3nx+4n
∵不含x3和x2项,
∴m=3,n=5,
故选C.
点评:此题主要考查了多项式乘以多项式,表示出x3和x2项的系数是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法:①0是整数;②4.2不是正数;③自然数一定是正数;④-2.5是负分数;⑤负分数一定是负有理数.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
一种面粉包装袋上的质量标识为“25±0.5kg”,则下列四袋面粉中不合格的是( )
| A、24.5kg |
| B、25.5kg |
| C、24.8kg |
| D、26.1kg |
方程x2-6x=0的解为( )
| A、x=0 |
| B、x=6 |
| C、x1=0,x2=-6 |
| D、x1=0,x2=6 |
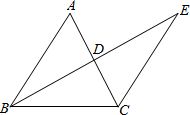 如图,BE⊥AC,垂足为D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=
如图,BE⊥AC,垂足为D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=