题目内容
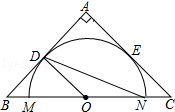 如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则∠MND的度数为
如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则∠MND的度数为考点:切线的性质,等腰直角三角形
专题:
分析:根据切线的性质即可求得∠BDO的度数,然后根据△ABC是等腰直角三角形,求得∠B的度数,则∠BOD的度数即可求解,然后根据圆周角定理即可求解.
解答:解:∵AB是圆的切线,
∴OD⊥AB,即∠BDO=90°,
又∵△ABC是等腰直角三角形,
∴∠B=45°,
∴∠BOD=45°,
∴∠MND=
∠BOD=22.5°.
故答案是:22.5.
∴OD⊥AB,即∠BDO=90°,
又∵△ABC是等腰直角三角形,
∴∠B=45°,
∴∠BOD=45°,
∴∠MND=
| 1 |
| 2 |
故答案是:22.5.
点评:本题考查了切线的性质定理以及圆周角定理,正确理解定理是关键.

练习册系列答案
相关题目
下列关于x的方程一定有实数解的是( )
A、
| ||||
B、
| ||||
| C、x2-x-1=0 | ||||
| D、x2-x+1=0 |
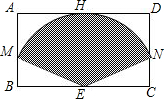 如图,矩形ABCD中,AB=4,BC=4
如图,矩形ABCD中,AB=4,BC=4
 函数y=kx+b的大致图象如图所示,则当x<0时,y的取值范围是
函数y=kx+b的大致图象如图所示,则当x<0时,y的取值范围是