题目内容
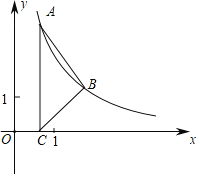
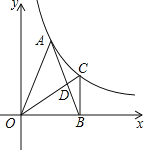
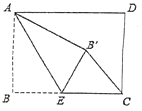
【题目】如图,角α的两边与双曲线y=![]() (k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=
(k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=![]() 、射线OA于点E、F,若OA=2AF,OC=2CB,则
、射线OA于点E、F,若OA=2AF,OC=2CB,则![]() 的值为______.
的值为______.
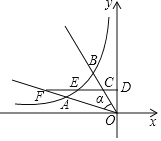
【答案】![]()
【解析】
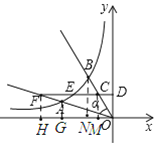
过C,B,A,F分别作CM⊥x轴,BN⊥x轴,AG⊥x轴,FH⊥x轴,设DO为2a,分别求出C,E,F的坐标,即可求出![]() 的值.
的值.
如图:过C,B,A,F分别作CM⊥x轴,BN⊥x轴,AG⊥x轴,FH⊥x轴,
设DO为2a,则E(![]() ,2a),
,2a),
∵BN∥CM,
∴△OCM∽△OBN,
∴![]() =
=![]() ,
,
∴BN=3a,
∴B(![]() ,3a),
,3a),
∴直线OB的解析式y=![]() x,
x,
∴C(![]() ,2a),
,2a),
∵FH∥AG,
∴△OAG∽△OFH,
∴![]() ,
,
∵FH=OD=2a,
∴AG=![]() a,
a,
∴A(![]() ,
,![]() a),
a),
∴直线OA的解析式y=![]() x,
x,
∴F(![]() ,2a),
,2a),
∴![]() =
=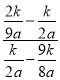 =
=![]() ,
,
故答案为:![]()

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目