题目内容
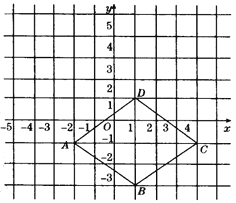
【题目】如图，四边形ABCD的四个顶点分别在反比例函数
与
(x＞0，0＜m＜n)的图象上，对角线BD//y轴，且BD⊥AC于点P．已知点B的横坐标为4．
（1）当m=4，n=20时．
①若点P的纵坐标为2，求直线AB的函数表达式．
②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．
（2）四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．
【答案】（1）①
；②四边形
是菱形，理由见解析；（2）四边形能是正方形，理由见解析，m+n=32.
【解析】
（1）①先确定出点A，B坐标，再利用待定系数法即可得出结论；
②先确定出点D坐标，进而确定出点P坐标，进而求出PA，PC，即可得出结论；
（2）先确定出B（4，
），D（4，
），进而求出点P的坐标，再求出A，C坐标，最后用AC=BD，即可得出结论．
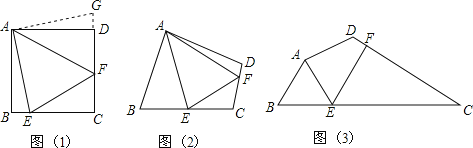
（1）①如图1，
，
反比例函数为
，
当
时，
，
，
当
时，
，
，
，
设直线
的解析式为
，
，
，
直线的解析式为
；
②四边形是菱形，
理由如下：如图2，
由①知，
，
轴，
，
点
是线段
的中点，
，
当
时，由得，
，
由
得，
，
，
，
，
，
四边形为平行四边形，
，
四边形是菱形；
（2）四边形能是正方形，
理由：当四边形是正方形，记
，的交点为，
,
当时，
，
，
，
，
，
，
，
，
，
.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
