题目内容
17.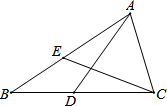 如图,点D在BC上,E在AB上,BD=BE,补充一个条件①AD=CE ②AE=CD ③∠BAD=∠BCE ④∠ADB=∠CEB,能证明△ADB≌△CEB的有( )个.
如图,点D在BC上,E在AB上,BD=BE,补充一个条件①AD=CE ②AE=CD ③∠BAD=∠BCE ④∠ADB=∠CEB,能证明△ADB≌△CEB的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由全等三角形的判定方法得出①不能证明;由SAS得出②能证明;由AAS得出③能证明;由ASA得出④能证明;即可得出结论.
解答 解:①不能;
∵BD=BE,AD=CE,∠B=∠B,
∴不能证明△ADB≌△CEB;
②能证明;
∵AE=CD,BD=BE,
∴AB=CB,
在△ADB和△CEB中,
$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠B=∠B}&{\;}\\{BD=BE}&{\;}\end{array}\right.$,
∴△ADB≌△CEB(SAS);
③能证明;
在△ADB和△CEB中,
$\left\{\begin{array}{l}{∠BAD=∠BCE}&{\;}\\{∠B=∠B}&{\;}\\{BD=BE}&{\;}\end{array}\right.$,
∴△ADB≌△CEB(AAS);
④能证明;
在△ADB和△CEB中,
$\left\{\begin{array}{l}{∠ADB=∠CEB}&{\;}\\{BD=BE}&{\;}\\{∠B=∠B}&{\;}\end{array}\right.$,
∴△ADB≌△CEB(ASA);
能证明△ADB≌△CEB的有3个,
故选:C.
点评 本题考查了全等三角形的判定方法;熟练掌握三角形全等的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5.下列计算错误的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C. | ${(\sqrt{3})^2}=3$ | D. | $(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})=1$ |
2.下列几何体中,不属于多面体的是( )
| A. | 六棱柱 | B. | 直三棱柱 | C. | 长方体 | D. | 圆柱 |
 如图,某校A距离公路3千米,又与该公路旁上的某车站D的距离为5千米,现在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离为$\frac{25}{8}$千米.
如图,某校A距离公路3千米,又与该公路旁上的某车站D的距离为5千米,现在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离为$\frac{25}{8}$千米.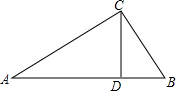 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为4.
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为4.