题目内容
8.观察下列各等式:$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…根据你发现的规律计算$\frac{-3}{1×2}$+$\frac{-3}{2×3}$+$\frac{-3}{3×4}$+…+$\frac{-3}{n(n+1)}$的结果为-$\frac{3n}{n+1}$(n为正整数).分析 首先提取-3,进一步利用给出的方法拆分计算得出答案即可.
解答 解:原式=-3[$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$]
=-3×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=-3×(1-$\frac{1}{n+1}$)
=-$\frac{3n}{n+1}$.
故答案为:-$\frac{3n}{n+1}$.
点评 此题考查有理数的混合运算,掌握拆分的方法是解决问题的关键.

练习册系列答案
相关题目
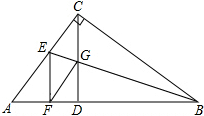 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F.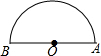 如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=180°-$\frac{1}{{2}^{n+1}}$×180°.
如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=180°-$\frac{1}{{2}^{n+1}}$×180°.