题目内容
20.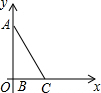 在Rt△ABC中,∠ABC=90°,AB=4,BC=2.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为2+2$\sqrt{2}$.
在Rt△ABC中,∠ABC=90°,AB=4,BC=2.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为2+2$\sqrt{2}$.
分析 根据题意首先取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,进而求出答案.
解答  解:如图所示:取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,在
解:如图所示:取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,在
Rt△A1OB1中,∵A1B1=AB=4,点OE为斜边中线,
∴OE=B1E=$\frac{1}{2}$A1B1=2,
又∵B1C1=BC=2,
∴C1E=$\sqrt{{B}_{1}{C}_{1}^{2}+{B}_{1}{E}^{2}}$=2$\sqrt{2}$,
∴点C到原点的最大距离为:OE+C1E=2+2$\sqrt{2}$.
故答案为:2+2$\sqrt{2}$.
点评 此题主要考查了轨迹以及勾股定理等知识,正确得出C点位置是解题关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,∠DAP=20°,PD⊥AB于D,PE⊥AC于E,且PD=PE,则∠BAC=40°.
如图,∠DAP=20°,PD⊥AB于D,PE⊥AC于E,且PD=PE,则∠BAC=40°. 如图,在菱形ABCD中,∠B=120°,AB=4cm,则这个菱形的周长是16cm,面积是8$\sqrt{3}$cm2.
如图,在菱形ABCD中,∠B=120°,AB=4cm,则这个菱形的周长是16cm,面积是8$\sqrt{3}$cm2. 如图,△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=75度.
如图,△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=75度.