题目内容
7．已知点A（-2，0），AB∥y轴，且AB=3，则B点坐标为（-2，3）或（-2，-3）．分析 先由AB∥y轴，可得A、B两点横坐标相等，再根据AB的长为3，分B点在A点上边和下边，分别求B点坐标即可．
解答 解：∵AB∥y轴，点A的坐标为（-2，0），
∴A、B两点横坐标都是-2，
又∵AB=3，
∴当B点在A点上边时，B的坐标为（-2，3），
当B点在A点下边时，B的坐标为（-2，-3）．
故答案为：（-2，3）或（-2，-3）．
点评 本题主要考查了：平行于x轴的直线上所有点纵坐标相等，根据A、B两点的距离及相对位置，分类求解．
练习册系列答案
教材全解字词句篇系列答案
相关题目
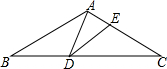如图，等腰△ABC的腰长为2$\sqrt{3}$，D为底边BC上一点，且BD=2，E为腰AC上一点，若∠ADE=∠B=30°，则CE的长为$\frac{4\sqrt{3}}{3}$．
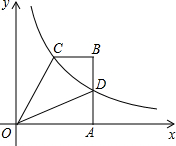四边形OABC中，BC∥OA，∠OAB=90°，OA=6，腰AB上有一点D，AD=3，四边形ODBC的面积为18，建立如图所示的平面直角坐标系，反比例函数y=$\frac{m}{x}$（x＞0）的图象恰好经过点C和点D．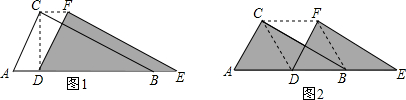
2．
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∠ACD=3∠BCD，E是斜边AB的中点，则∠ECD=（ ）
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∠ACD=3∠BCD，E是斜边AB的中点，则∠ECD=（ ）| A． | 22.5° | B． | 30° | C． | 36° | D． | 45° |
19．用配方法将x2-2x-2=0变形，正确的是（ ）
| A． | （x-1）2=1 | B． | （x+1）2=3 | C． | （x-1）2=3 | D． | （x+1）2=1 |
如图，等腰△ABC的周长为19，底边BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为12．