题目内容
5. 已知二次函数y=x2+bx-4的图象与y轴交于点C,与x轴的正半轴交于点A,且tan∠ACO=$\frac{1}{4}$.请解答下列问题:
已知二次函数y=x2+bx-4的图象与y轴交于点C,与x轴的正半轴交于点A,且tan∠ACO=$\frac{1}{4}$.请解答下列问题:(1)求二次函数的解析式;
(2)P为二次函数图象的顶点,Q为其对称轴上的一点,QC平分∠PQO,求Q点坐标.
分析 (1)首先根据tan∠ACO的值,求出OA的值,即可判断出A点的坐标;然后把A点的坐标代入y=x2+bx-4,求出b的值,即可判断出二次函数的解析式.
(2)首先根据Q为抛物线对称轴上的一点,设点Q的坐标为(-1.5,n);然后根据∠OQC=∠CQP、∠CQP=∠OCQ,可得∠OQC=∠OCQ,所以OQ=OC,据此求出n的值,进而判断出Q点坐标即可.
解答 解:(1)如图1,连接AC,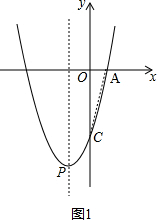 ,
,
∵二次函数y=x2+bx-4的图象与y轴的交点为C,
∴C点的坐标为(0,-4),
∵tan∠ACO=$\frac{1}{4}$,
∴$\frac{OA}{OC}=\frac{1}{4}$,
又∵OC=4,
∴OA=1,
∴A点的坐标为(1,0),
把A(1,0)代入y=x2+bx-4,
可得0=1+b-4,
解得b=3,
∴二次函数的解析式是:y=x2+3x-4.
(2)如图2,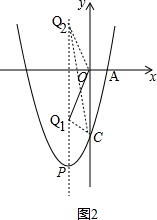 ,
,
∵y=x2+3x-4,
∴抛物线的对称轴是:x=-1.5,
∵Q为抛物线对称轴上的一点,
∴设点Q的坐标为(-1.5,n),
∵抛物线的对称轴平行于y轴,
∴∠CQP=∠OCQ,
又∵∠OQC=∠CQP,
∴∠OQC=∠OCQ,
∴OQ=OC,
∴$\sqrt{(-\frac{3}{2})^{2}+{n}^{2}}$=4,
解得n=±$\frac{\sqrt{55}}{2}$,
∴Q点坐标是(-1.5,$\frac{\sqrt{55}}{2}$)或(-1.5,-$\frac{\sqrt{55}}{2}$).
点评 此题主要考查了用待定系数法求二次函数的解析式的方法,考查了学生分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.

练习册系列答案
相关题目
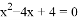 的根的情况是 ( )
的根的情况是 ( )
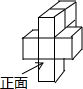 如果用□表示1个立方体,用
如果用□表示1个立方体,用 表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )

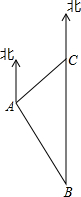 海上有两个灯塔B,C,其中灯塔C位于灯塔B的正北方向20海里处,在点A处测得灯塔C位于A的东北方向上,A位于灯塔B的北偏西30°方向上,点A与灯塔C之间的距离是多少?(结果精确到0.1海里.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
海上有两个灯塔B,C,其中灯塔C位于灯塔B的正北方向20海里处,在点A处测得灯塔C位于A的东北方向上,A位于灯塔B的北偏西30°方向上,点A与灯塔C之间的距离是多少?(结果精确到0.1海里.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)