题目内容
8.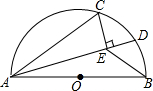 如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是$\widehat{BC}$上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为$\sqrt{13}$-2.
如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是$\widehat{BC}$上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为$\sqrt{13}$-2.
分析 如图,连接BO′、BC.在点D移动的过程中,点E在以AC为直径的圆上运动,当O′、E、B共线时,BE的值最小,最小值为O′B-O′E,利用勾股定理求出BO′即可解决问题.
解答 解:如图,连接BO′、BC.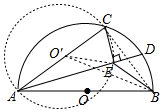
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4,AB=5,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
在Rt△BCO′中,BO′=$\sqrt{B{C}^{2}+CO{′}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∵O′E+BE≥O′B,
∴当O′、E、B共线时,BE的值最小,最小值为O′B-O′E=$\sqrt{13}$-2,
故答案为:$\sqrt{13}-2$.
点评 本题考查圆综合题、勾股定理、点与圆的位置关系等知识,解题的关键是确定等E的运动轨迹是以AC为直径的圆上运动,属于中考填空题中 压轴题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后水龙头滴下的水为(用科学记数法表示)( )
| A. | 1440毫升 | B. | 1.4×103毫升 | C. | 0.14×104毫升 | D. | 14×102毫升 |
15.已知关于x,y的方程xm-2+4ym+n=6是二元一次方程,则m,n的值为( )
| A. | m=1,n=0 | B. | m=3,n=-4 | C. | m=1,n=-2 | D. | m=3,n=-2 |
 如图,已知AD∥BC,A,B,E在一条直线上,∠1=60°,∠2=45°,则∠A=60°,∠BDA=75°.
如图,已知AD∥BC,A,B,E在一条直线上,∠1=60°,∠2=45°,则∠A=60°,∠BDA=75°.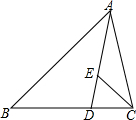 在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5$\sqrt{2}$.AE=2DE,则AC=$\sqrt{26}$.
在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5$\sqrt{2}$.AE=2DE,则AC=$\sqrt{26}$. 探测船上的声呐发出的超声波以1450m/s的速度射向海底,海底再将超声波反射回来,经ts后声呐收到反射超声波.试求海底深度hm与时间ts之间的关系.
探测船上的声呐发出的超声波以1450m/s的速度射向海底,海底再将超声波反射回来,经ts后声呐收到反射超声波.试求海底深度hm与时间ts之间的关系.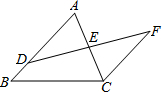 已知:如图,△ABC中,点D,E分别在AB,AC上,CF∥AB交DE的延长线于点F,DE=EF,DB=3,CF=5,则AB=8.
已知:如图,△ABC中,点D,E分别在AB,AC上,CF∥AB交DE的延长线于点F,DE=EF,DB=3,CF=5,则AB=8.