题目内容
9.【问题情境】张老师给爱好学习的小林和小兰提出这样一个问题:如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
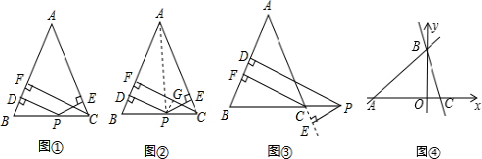
小林的证明思路是:如图②,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小兰的证明思路是:如图②,过点P作PG⊥CF,垂足为G,通过证明四边形PDFG是矩形,
可得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
【结论运用】请运用上述解答中所积累的经验和方法完成下列两题:
如图④,在平面直角坐标系中有两条直线l1:y=$\frac{3}{4}$x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述的结论求出点M的坐标.
分析 【问题情境】利用小林或小兰的思路可以证明;
【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;
【结论运用】分M在线段BC上和M在线段BC外两种情况,再分别根据△AMC和△AMB的面积和与差等于△ABC的面积,求得M到AC的距离,即M点的纵坐标,再代入l2的解析式可求出M的坐标.
解答 解:【问题情境】
如图②,连接AP,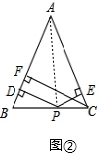
∵PD⊥AB,PE⊥AC,CF⊥AB,
∴S△ABP=$\frac{1}{2}$AB•PD,S△ACP=$\frac{1}{2}$AC•PE,S△ABC=$\frac{1}{2}$AB•CF,
∵S△ABP+S△ACP=S△ABC,
∴$\frac{1}{2}$AB•PD+$\frac{1}{2}$AC•PE=$\frac{1}{2}$AB•CF,
又AB=AC,
∴PD+PE=CF;
【变式探究】
如图3,连接AP,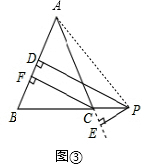
∵PD⊥AB,PE⊥AC,CF⊥AB,
∴S△ABP=$\frac{1}{2}$AB•PD,S△ACP=$\frac{1}{2}$AC•PE,S△ABC=$\frac{1}{2}$AB•CF,
∵S△ABP-S△ACP=S△ABC,
∴$\frac{1}{2}$AB•PD-$\frac{1}{2}$AC•PE=$\frac{1}{2}$AB•CF,
又∵AB=AC,
∴PD-PE=CF;
【结论运用】
由题意可求得A(-4,0),B(3,0),C(0,1),
∴AB=5,AC=5,BC=$\sqrt{10}$,OB=3,
当M在线段BC上时,过M分别作MP⊥x轴,MQ⊥AB,垂足分别为P、Q,如图④,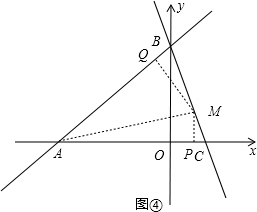
则S△AMC=$\frac{1}{2}$AC•MP,S△AMB=$\frac{1}{2}$AB•MQ,S△ABC=$\frac{1}{2}$OB•AC,
∵S△AMC+S△AMB=S△ABC,
∴$\frac{1}{2}$AC•MP+$\frac{1}{2}$AB•MQ=$\frac{1}{2}$OB•AC,
即$\frac{1}{2}$×5×MP+$\frac{1}{2}$×5×1=$\frac{1}{2}$×3×5,解得MP=2,
∴M点的纵坐标为2,
又∵M在直线y=-3x+3,
∴当y=2时,代入可求得x=$\frac{1}{3}$,
∴M坐标为($\frac{1}{3}$,2);
同理,由前面结论可知当M点在线段BC外时,有|MP-MQ|=OB,
可求得MP=4或MP=-2,即M点的纵坐标为4或-2,
分别代入y=-3x+3,可求得x=-$\frac{1}{3}$或x=$\frac{5}{3}$(舍,因为它到l1的距离不是1),
∴M点的坐标为(-$\frac{1}{3}$,4);
综上可知M点的坐标为($\frac{1}{3}$,2)或(-$\frac{1}{3}$,4).
点评 本题主要考查一次函数的综合运用,涉及等腰三角形的性质、三角形的面积、勾股定理和等积法等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.

| A. | (-4,0) | B. | (6,0) | C. | (-4,0)或(6,0) | D. | (0,12)或(0,-8) |
| A. | x-2x=x | B. | x6÷x3=x2 | C. | (-x2)3=-x6 | D. | (x+y)2=x2+y2 |
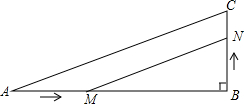 如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.
如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2. 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.
如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.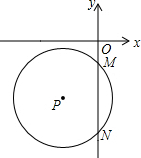 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=-2x+m图象过点P,则m=-15.
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=-2x+m图象过点P,则m=-15.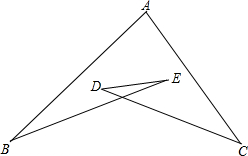 如图,∠A+∠B+∠C+∠D+∠E=180°.
如图,∠A+∠B+∠C+∠D+∠E=180°.