题目内容
16.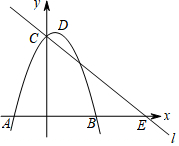 如图,抛物线y=-x2+x+6与x轴交于A,B两点,点A在点B的左侧,抛物线与y轴交于C,抛物线的顶点为D,直线l过点C交x轴于E(6,0).
如图,抛物线y=-x2+x+6与x轴交于A,B两点,点A在点B的左侧,抛物线与y轴交于C,抛物线的顶点为D,直线l过点C交x轴于E(6,0).(1)写出顶点D的坐标和直线l的解析式.
(2)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于NN连接CN,将△CMN沿CN翻转,M的对应点为M′.探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
分析 (1)利用y轴上点的坐标特征写出C(0,6),再利用配方法得到D点坐标,然后利用待定系数法求直线l的解析式;
(2)直线CN交x轴于P,作PH⊥l于H,如图,线CN交x轴于P,作PH⊥l于H,如图,利用折叠的性质得CN平分∠MCM′,则根据角平分线的性质得PO=PH,设OP=t,则PH=t,PE=6-t,证明△PEH为等腰直角三角形得到6-t=$\sqrt{2}$t,解得t=6($\sqrt{2}$+1),则P(6($\sqrt{2}$+1),0),接着利用待定系数法求出直线PC的解析式为y=-($\sqrt{2}$+1)x+6,然后解方程组$\left\{\begin{array}{l}{y=-{x}^{2}+x+6}\\{y=-(\sqrt{2}+1)x+6}\end{array}\right.$得N点坐标,从而得到Q点坐标.
解答 解:(1)当x=0时,y=-x2+x+6=6,则C(0,6),
y=-x2+x+6=-(x-$\frac{1}{2}$)2+$\frac{23}{4}$,则D点坐标为($\frac{1}{2}$,$\frac{23}{4}$),
设直线l的解析式为y=kx+b,
把C(0,6),E(6,0)代入得$\left\{\begin{array}{l}{6k+b=0}\\{b=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴直线l的解析式为y=-x+6;
(2)存在.
直线CN交x轴于P,作PH⊥l于H,如图,利用折叠的性质得CN平分∠MCM′,则根据角平分线的性质得PO=PH,
设OP=t,则PH=t,PE=6-t,
∵OC=OE,
∴△OCE为等腰直角三角形,
∴∠PEH=45°,
∴△PEH为等腰直角三角形,
∴PE=$\sqrt{2}$PH,即6-t=$\sqrt{2}$t,解得t=6($\sqrt{2}$+1),
∴P(6($\sqrt{2}$+1),0),
设直线PC的解析式为y=mx+n,
把C(0,6),P(6($\sqrt{2}$+1),0)代入得$\left\{\begin{array}{l}{n=6}\\{6(\sqrt{2}+1)m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-(\sqrt{2}+1)}\\{n=6}\end{array}\right.$,
∴直线PC的解析式为y=-($\sqrt{2}$+1)x+6,
解方程组$\left\{\begin{array}{l}{y=-{x}^{2}+x+6}\\{y=-(\sqrt{2}+1)x+6}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=2+\sqrt{2}}\\{y=2-3\sqrt{2}}\end{array}\right.$,
∴N(2+$\sqrt{2}$,2-3$\sqrt{2}$),
∴QN⊥x轴,
∴Q(2+$\sqrt{2}$,0).
点评 本题考查了二次函数的综合题:熟练掌握角平分线的性质、折叠的性质和二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求一次函数的解析式,能利用解方程组求抛物线与直线的交点坐标;理解坐标与图形性质.

| A. | m=1 | B. | m=-1 | C. | m=$\frac{1}{2}$ | D. | m=0 |
| A. | 3-x2 | B. | 9+x2 | C. | x2-9 | D. | 3+x2 |
| A. | 5a2+3a2=8a4 | B. | a3•a4=a12 | C. | (a+2b)2=a2+4b2 | D. | -$\root{3}{125}$=-5 |
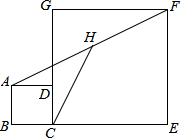 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$. 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法:
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法: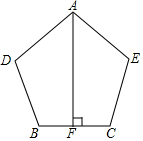 如图.AD=AE.BD=CE,AF⊥BC于点F,且F是BC的中点,求证:∠D=∠E.
如图.AD=AE.BD=CE,AF⊥BC于点F,且F是BC的中点,求证:∠D=∠E.