题目内容
 抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.(1)求出m的值并在给出的直角坐标系中画出这条抛物线;
(2)根据图象回答下列问题:
①方程-x2+(m-1)x+m=0的根是多少?
②x取什么值时,y<0?
考点:二次函数的图象,抛物线与x轴的交点,二次函数与不等式(组)
专题:
分析:(1)把点(0,3)代入y=-x2+(m-1)x+m,即可求出m的值.利用五点画出函数的图象;
(2)根据方程-x2+(m-1)x+m=0的根就是函数值为0抛物线和x轴的交点的横坐标,观察图形可直接得出方程的根以及y<0时,x的取值范围.
(2)根据方程-x2+(m-1)x+m=0的根就是函数值为0抛物线和x轴的交点的横坐标,观察图形可直接得出方程的根以及y<0时,x的取值范围.
解答:解:(1)∵y=-x2+(m-1)x+m与y轴交于点(0,3)
∴m=3,
∴抛物线的表达式为:y=-x2+2x+3=-(x-1)2+4.
∴顶点(1,4),
列表:

描点、连线可得如图所示抛物线.
(2)①由图象可知,抛物线与x轴交点为(-1,0),(3,0),
∴方程=-x2+(m-1)x+m=0的解为x1=-1,x2=3,
②由图象可知,当x<-1或>3时y<0.
∴m=3,
∴抛物线的表达式为:y=-x2+2x+3=-(x-1)2+4.
∴顶点(1,4),
列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | … |

描点、连线可得如图所示抛物线.
(2)①由图象可知,抛物线与x轴交点为(-1,0),(3,0),
∴方程=-x2+(m-1)x+m=0的解为x1=-1,x2=3,
②由图象可知,当x<-1或>3时y<0.
点评:本题考查了函数图象上的点的坐标与函数解析式的关系,关键是根据题意画出图形,根据抛物线解析式求出抛物线的顶点坐标,对称轴及与x轴的交点坐标.

练习册系列答案
相关题目
在-3.14159…,2.
,
,
,
,-
中,无理数有( )个.
| • |
| 1 |
| π |
| 2 |
| 1.6 |
| 11 |
| 5 |
| 3 | 0.001 |
| A、2 | B、3 | C、4 | D、5 |
光年天文学中的距离单位,1光年大约是9500000000000km,用科学记数法表示为( )
| A、950×1010km |
| B、95×1012km |
| C、9.5×1012km |
| D、0.95×1013km |
 如图,点C在线段AB上,且AC=6,BC=14,点M,N分别是AC,BC的中点,则线段MN的长度为( )
如图,点C在线段AB上,且AC=6,BC=14,点M,N分别是AC,BC的中点,则线段MN的长度为( )| A、10 | B、20 | C、7 | D、8 |
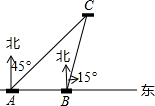 马航失联客机MH370引起全球高度关注,为了搜寻客机残骸,我国派出多艘军舰和海监船到达失事海域进行搜寻,如图,前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行,B舰在A舰的正东方向,且亮剑保持20海里的距离,某一时刻两舰同时测得在A的东北方向,B的北偏东15°方向有一艘澳方军舰C,求此时舰C与我舰航线AB的距离是多少?(结果保留根号)
马航失联客机MH370引起全球高度关注,为了搜寻客机残骸,我国派出多艘军舰和海监船到达失事海域进行搜寻,如图,前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行,B舰在A舰的正东方向,且亮剑保持20海里的距离,某一时刻两舰同时测得在A的东北方向,B的北偏东15°方向有一艘澳方军舰C,求此时舰C与我舰航线AB的距离是多少?(结果保留根号) 如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.
如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC. 如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )
如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )