题目内容
 如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.
如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.(1)∠FBC与∠ABC的数量关系是
(2)如果BE是∠FBD的平分线,那么BE与BC有怎样的位置关系?为什么?
(3)在(2)的条件下,将BE沿BF折叠使其落在∠FBC的内部,交CF于点M.若BM平分∠FBC,求∠FBE的度数.
考点:角的计算,角平分线的定义,翻折变换(折叠问题)
专题:计算题
分析:(1)由折叠的性质可得∠FBC与∠ABC是相等的;
(2)由(1)知∠FBC=∠ABC,再根据角平分线的定义可得∠FBE=
∠FBD,∠FBC=
∠ABF,再结合平角等于1800,即可推得结论;
(3)根据角平分线和折叠的性质,找出角与角之间的关系,列方程解答.
(2)由(1)知∠FBC=∠ABC,再根据角平分线的定义可得∠FBE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据角平分线和折叠的性质,找出角与角之间的关系,列方程解答.
解答:解:(1)等于;
(2)因为BE是∠FBD的平分线,
所以∠FBE=
∠FBD,
因为∠FBC=∠ABC,
所以∠FBC=
∠ABF,
所以∠FBE+∠FBC=
(∠FBD+∠ABF),
因为∠FBD+∠ABF=180°,
所以∠FBE+∠FBC=90°
所以∠CBE=90°,
所以BE⊥BC.
(3)设∠FBE=x,
因为BE是∠FBD的平分线,
所以∠EBD=x,
因为BM平分∠FBC,
所以∠FBC=2x,
因为∠FBC=∠ABC,
所以∠ABC=2x,
所以x+x+2x+2x=180°,
所以x=30°,
所以∠FBE=30°.
(2)因为BE是∠FBD的平分线,
所以∠FBE=
| 1 |
| 2 |
因为∠FBC=∠ABC,
所以∠FBC=
| 1 |
| 2 |
所以∠FBE+∠FBC=
| 1 |
| 2 |
因为∠FBD+∠ABF=180°,
所以∠FBE+∠FBC=90°
所以∠CBE=90°,
所以BE⊥BC.
(3)设∠FBE=x,
因为BE是∠FBD的平分线,
所以∠EBD=x,
因为BM平分∠FBC,
所以∠FBC=2x,
因为∠FBC=∠ABC,
所以∠ABC=2x,
所以x+x+2x+2x=180°,
所以x=30°,
所以∠FBE=30°.
点评:此题考查了折叠的性质,解答本题的关键是根据折叠的性质得出∠ABC=∠FBC,∠MBF=∠FBE,解答是要注意仔细观察所给图形.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
下列各式中正确的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
当x=-2
,y=-1
时,代数式x2+y2和代数式-2xy的值分别为M、N,则M、N之间的关系为( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、M<N | B、M=N |
| C、M>N | D、以上三种情况均有可能 |
 抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=
如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=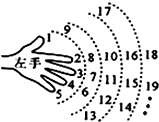 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2014时,对应的手指是( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2014时,对应的手指是( )