题目内容
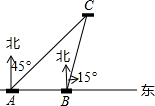 马航失联客机MH370引起全球高度关注,为了搜寻客机残骸,我国派出多艘军舰和海监船到达失事海域进行搜寻,如图,前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行,B舰在A舰的正东方向,且亮剑保持20海里的距离,某一时刻两舰同时测得在A的东北方向,B的北偏东15°方向有一艘澳方军舰C,求此时舰C与我舰航线AB的距离是多少?(结果保留根号)
马航失联客机MH370引起全球高度关注,为了搜寻客机残骸,我国派出多艘军舰和海监船到达失事海域进行搜寻,如图,前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行,B舰在A舰的正东方向,且亮剑保持20海里的距离,某一时刻两舰同时测得在A的东北方向,B的北偏东15°方向有一艘澳方军舰C,求此时舰C与我舰航线AB的距离是多少?(结果保留根号)考点:解直角三角形的应用-方向角问题
专题:
分析:作BD⊥AC于D,CH⊥AB于H,先根据勾股定理求出∠ACB的度数,再根据∠BAC=45°可知AD=BD=AB•sin∠BAD,同理可得出CD的长,进而可得出结论.
解答: 解:作BD⊥AC于D,CH⊥AB于H
解:作BD⊥AC于D,CH⊥AB于H
∵∠BAC=45°,∠ABC=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°
在Rt△ABD中,
AD=BD=AB•sin∠BAD=20×
=10
(海里)
在Rt△BCD中,CD=
=
=
(海里).
∴AC=AD+CD=10
+
在Rt△ACH中,CH=
×(10
+
)=10+
.
答:此时船C与航线AB的距离是(10+
)海里.
 解:作BD⊥AC于D,CH⊥AB于H
解:作BD⊥AC于D,CH⊥AB于H∵∠BAC=45°,∠ABC=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°
在Rt△ABD中,
AD=BD=AB•sin∠BAD=20×
| ||
| 2 |
| 2 |
在Rt△BCD中,CD=
| BD |
| COS∠BCD |
10
| ||||
|
20
| ||
| 3 |
∴AC=AD+CD=10
| 2 |
20
| ||
| 3 |
在Rt△ACH中,CH=
| ||
| 2 |
| 2 |
20
| ||
| 3 |
20
| ||
| 3 |
答:此时船C与航线AB的距离是(10+
20
| ||
| 3 |
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
当x=-2
,y=-1
时,代数式x2+y2和代数式-2xy的值分别为M、N,则M、N之间的关系为( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、M<N | B、M=N |
| C、M>N | D、以上三种情况均有可能 |
 抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=
如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= 如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一颗被风吹斜的柏树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB是多少米.
如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一颗被风吹斜的柏树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB是多少米.