题目内容
 四边形ABCD中,AD∥BC,且AB+BC=AD+DC,试说明四边形ABCD的是平行四边形.
四边形ABCD中,AD∥BC,且AB+BC=AD+DC,试说明四边形ABCD的是平行四边形.考点:平行四边形的判定
专题:
分析:首先延长AD,在AD延长线上截取DE=DC,延长BC,在BC延长线上截取AB=FC,进而得出△DEC≌△FCE(ASA),进而得出DC=EF,AD=BC,得出答案即可.
解答: 解:延长AD,在AD延长线上截取DE=DC,延长BC,在BC延长线上截取AB=FC,
解:延长AD,在AD延长线上截取DE=DC,延长BC,在BC延长线上截取AB=FC,
∵AB+BC=AD+DC,
∴AE=BF,
∵AD∥BC,
∴四边形ABFE是平行四边形,
∴AB=EF,
∵AE∥BF,
∴∠1=∠2,
∵DC=DE,FC=EF,
∴∠DCE=∠1,∠2=∠FEC,
在△DEC和△FCE中
,
∴△DEC≌△FCE(ASA),
∴DC=EF,
∴AD=BC,
∴四边形ABCD的是平行四边形.
 解:延长AD,在AD延长线上截取DE=DC,延长BC,在BC延长线上截取AB=FC,
解:延长AD,在AD延长线上截取DE=DC,延长BC,在BC延长线上截取AB=FC,∵AB+BC=AD+DC,
∴AE=BF,
∵AD∥BC,
∴四边形ABFE是平行四边形,
∴AB=EF,
∵AE∥BF,
∴∠1=∠2,
∵DC=DE,FC=EF,
∴∠DCE=∠1,∠2=∠FEC,
在△DEC和△FCE中
|
∴△DEC≌△FCE(ASA),
∴DC=EF,
∴AD=BC,
∴四边形ABCD的是平行四边形.
点评:此题主要考查了平行四边形的判定和全等三角形的判定与性质等知识,得出△DEC≌△FCE是解题关键.

练习册系列答案
相关题目
在平面直角坐标系中,下列坐标所对应的点位于第三象限的是( )
| A、(3,1) |
| B、(3,-1) |
| C、(-3,1) |
| D、(-3,-1) |
 如图,AB、CD是⊙O的两条直径,E、F是AB上两点,连接CE、DF,且满足CE∥DF,说明OE=OF的理由.
如图,AB、CD是⊙O的两条直径,E、F是AB上两点,连接CE、DF,且满足CE∥DF,说明OE=OF的理由.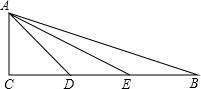 如图,在Rt△ABC中,∠C=90°,E、D为CB边的三等分点,且AC=CD=
如图,在Rt△ABC中,∠C=90°,E、D为CB边的三等分点,且AC=CD= 如图:是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对面上的汉字是
如图:是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对面上的汉字是