题目内容
15. 如图,△ABC中,DE∥BC,分别交BA,CA的延长线于D、E,EF∥CD交AB于F,求证:AD2=AF•AB.
如图,△ABC中,DE∥BC,分别交BA,CA的延长线于D、E,EF∥CD交AB于F,求证:AD2=AF•AB.
分析 如图,首先证明△ADE∽△ABC,得到$\frac{AB}{AD}=\frac{AC}{AE}$;同理可证△AEF∽△ACD,得到$\frac{AD}{AF}=\frac{AB}{AD}$,即可解决问题.
解答  证明:如图,∵DE∥BC,
证明:如图,∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AB}{AD}=\frac{AC}{AE}$;
同理可证:$\frac{AD}{AF}=\frac{AC}{AE}$,
∴$\frac{AD}{AF}=\frac{AB}{AD}$,
∴AD2=AF•AB.
点评 该题主要考查了相似三角形的判定及其性质的应用问题;牢固掌握相似三角形的判定及其性质是灵活运用、解题的基础和关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.若一个圆锥的侧面展开图是一个半径为10cm,圆心角为252°的扇形,则该圆锥的底面半径为( )
| A. | 6cm | B. | 7cm | C. | 8cm | D. | 10cm |
7. 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )
 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )| A. | 80° | B. | 100° | C. | 112° | D. | 132° |
 如图,四边形ABCD是⊙O的内接四边形,∠CBE是它的外角,若∠D=120°,则∠CBE的度数是120°.
如图,四边形ABCD是⊙O的内接四边形,∠CBE是它的外角,若∠D=120°,则∠CBE的度数是120°.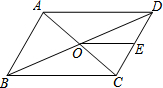 如图,已知?ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则?ABCD的周长为36cm.
如图,已知?ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则?ABCD的周长为36cm.