题目内容
6.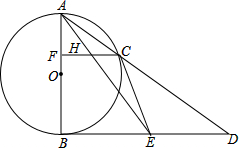 如图,已知C是以AB为直径的圆O上一点,CF⊥AB于点F,直线AC与过点B的切线相交于点D,E为BD的中点,连接AE交CF于点H,连接CE.
如图,已知C是以AB为直径的圆O上一点,CF⊥AB于点F,直线AC与过点B的切线相交于点D,E为BD的中点,连接AE交CF于点H,连接CE.(1)求证:点H是CF中点;
(2)求证:CH是⊙O的切线;
(3)若⊙O的半径为3,BE=4,求CF的长.
分析 (1)根据切线的性质得AB⊥BD,而CF⊥AB,所以CF∥BD,根据相似的判定方法得△AFH∽△ABE,△AHC∽△AED,利用相似的性质得$\frac{FH}{BE}$=$\frac{AH}{AE}$,$\frac{CH}{DE}$=$\frac{AH}{AE}$,所以$\frac{FH}{BE}$=$\frac{CH}{DE}$,而BE=DE,则FH=CH;
(2)根据圆周角定理由AB为⊙的直径得∠ACB=90°,则∠BCD=90°,而CE为BD边上的中线,根据直角三角形斜边上的中线性质得CE=BE=DE,则∠2=∠3,而∠1=∠4,所以有∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,则OC⊥CE,然后根据切线的判定定理得CE是⊙O的切线;
(3)先计算出BD=2BE=6,在Rt△ABD中,根据勾股定理计算出AD=10,再证明Rt△ABC∽Rt△ADB,利用相似比计算出AC=$\frac{18}{5}$,然后证明△ACF∽△ADB,利用相似比可计算出CF=$\frac{72}{25}$.
解答 (1)证明:∵BD为⊙的切线,
∴AB⊥BD,
∵CF⊥AB,
∴CF∥BD,
∴△AFH∽△ABE,△AHC∽△AED,
∴$\frac{FH}{BE}$=$\frac{AH}{AE}$,$\frac{CH}{DE}$=$\frac{AH}{AE}$,
∴$\frac{FH}{BE}$=$\frac{CH}{DE}$,
而E为BD中点,
∴BE=DE,
∴FH=CH,
即点H是CF中点;
(2)证明:∵AB为⊙的直径,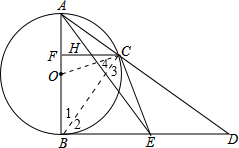 ∴∠ACB=90°,
∴∠ACB=90°,
∴∠BCD=90°,
而CE为BD边上的中线,
∴CE=BE=DE,
∴∠2=∠3,
∵OB=OC,
∴∠1=∠4,
∴∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(3)解:∵BE=4,
∴BD=2BE=8,
在Rt△ABD中,AB=6,
∴AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=10,
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴$\frac{AC}{AB}$=$\frac{AB}{AD}$,即$\frac{AC}{6}$=$\frac{6}{10}$,
∴AC=$\frac{18}{5}$,
∵CF∥BD,
∴△ACF∽△ADB,
∴$\frac{CF}{BD}$=$\frac{AC}{AD}$,即$\frac{CF}{8}$=$\frac{\frac{18}{5}}{10}$,
∴CF=$\frac{72}{25}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质、圆周角定理和勾股定理.

 名题金卷系列答案
名题金卷系列答案| A. | -2 | B. | -$\sqrt{5}$ | C. | -1 | D. | 0 |
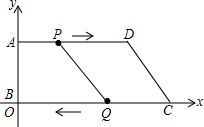 如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.
如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.