阅读理解并解答:为了求1+2+22+23+24+-+22013的值．可令S=1+2+22+23+24+-+22013.则2S=2+22+23+24+25+-+22013+22014因此2S-S=(2+22+23+-+22013+22014)-(1+2+22+23+-+22013)=22014-1．所以:S=22014-1．即1+2+22+23+24+-+22013=22014-1．请依照题目和参考答案——青夏教育精英家教网—

题目内容

5．阅读理解并解答：为了求1+2+2²+2³+2⁴+…+2²⁰¹³的值．
可令S=1+2+2²+2³+2⁴+…+2²⁰¹³，则2S=2+2²+2³+2⁴+2⁵+…+2²⁰¹³+2²⁰¹⁴
因此2S-S=（2+2²+2³+…+2²⁰¹³+2²⁰¹⁴）-（1+2+2²+2³+…+2²⁰¹³）=2²⁰¹⁴-1．
所以：S=2²⁰¹⁴-1．即1+2+2²+2³+2⁴+…+2²⁰¹³=2²⁰¹⁴-1．
请依照此法，求：1+5+5²+5³+5⁴+…+5²⁰¹⁶的值．

分析根据题目信息，设S=1+5+5²+5³+…+5²⁰¹⁶，求出5S，然后相减计算即可得解．

解答解：设S=1+5+5²+5³+…+5²⁰¹⁶，
则5S=5+5²+5³+5⁴…+5²⁰¹⁷，
两式相减得：4S=5²⁰¹⁷-1，
则S=$\frac{{5}^{2017}-1}{4}$．
∴1+5+5²+5³+5⁴+…+5²⁰¹⁶的值为$\frac{{5}^{2017}-1}{4}$．

点评本题考查了有理数的乘方，读懂题目信息，理解求和的运算方法是解题的关键．

练习册系列答案

毕业总复习高分策略指导与实战训练系列答案

创优考100分系列答案

高分中考系列答案

16．

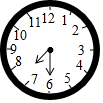如图，当时钟显示7：30分时，时针与分针的夹角为45°．

13．

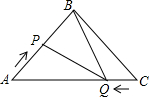如图，在△ABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x秒．
（1）当CQ=10时，求$\frac{{S}_{△APQ}}{{S}_{△PQB}}$的值．
（2）当x为何值时，PQ∥BC；
（3）是否存在某一时刻，使△APQ与△CQB相似？若存在，求出此时AP的长，若不存在，请说明理由．

20．关于x的方程3x-2k=3的解是-1，则k的值是-3．

10．（1）计算：$\sqrt{3}$sin60°-$\sqrt{2}$cos45°+tan²30°；
（2）若$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$≠0，求$\frac{2x+3y}{z}$的值．

17．若关于x的分式方程$\frac{x}{x-3}$-2=$\frac{{m}^{2}}{x-3}$有增根，则m^-2的值为$\frac{1}{3}$．

14．

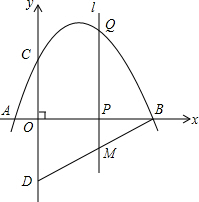如图，抛物线y=-$\frac{1}{2}$x²+$\frac{5}{2}$x+3 与 x 轴交于点 A，点 B，与 y 轴交于点C，点D 与点C关于 x 轴对称，点 P 是 x 轴上的一个动点，设点P 的坐标为（m，0），过点 P 作 x 轴的垂线 l 交抛物线于点 Q．
（1）求直线BD的解析式；
（2）当点P在线段OB上运动时，直线 l 交 BD 于点M，当△DQB面积最大时，在x轴上找一点E，使QE+$\frac{\sqrt{5}}{5}$EB的值最小，求E的坐标和最小值．
（3）在点P的运动过程中，是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

15．下列判断中正确的是（　　）

	A．	长度相等的弧是等弧
	B．	平分弦的直线也必平分弦所对的两条弧
	C．	弦的垂直平分线必平分弦所对的两条弧
	D．	平分一条弧的直线必平分这条弧所对的弦

试题分类