题目内容
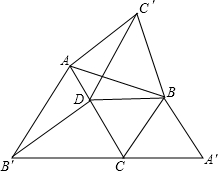 如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC(1)证明:△C′BD≌△B′DC;
(2)证明:△AC′D≌△DB′A.
考点:全等三角形的判定,等边三角形的性质
专题:证明题
分析:(1)根据SAS先证出△C′BD≌△ABC,再根据SAS证出△ABC≌△B′DC即可;
(2)根据(1)的结论,利用SSS证出△AC′D≌△DB′A即可.
(2)根据(1)的结论,利用SSS证出△AC′D≌△DB′A即可.
解答:解:(1)∵∠DBC=60°,
∴∠C′BD=60°+∠ABD=∠ABC,
在△C′BD与△ABC中,
,
∴△C′BD≌△ABC(SAS),
∴C′D=AC,
在△BCA与△DCB′中,
,
∴△BCA≌△DCB′(SAS).
∴DB′=BA,
∴△C′BD≌△B′DC.
(2)由(1)的结论知:
C′D=B′C=AB′,
B′D=BC′=AC′,
又∵AD=AD,
在△AC′D与△DB′A中,
,
∴△AC′D≌△DB′A(SSS).
∴∠C′BD=60°+∠ABD=∠ABC,
在△C′BD与△ABC中,
|
∴△C′BD≌△ABC(SAS),
∴C′D=AC,
在△BCA与△DCB′中,
|
∴△BCA≌△DCB′(SAS).
∴DB′=BA,
∴△C′BD≌△B′DC.
(2)由(1)的结论知:
C′D=B′C=AB′,
B′D=BC′=AC′,
又∵AD=AD,
在△AC′D与△DB′A中,
|
∴△AC′D≌△DB′A(SSS).
点评:此题考查了全等三角形的判定和等边三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
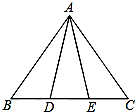 如图,点D、E在△ABC的边BC上,连接AD、AE.①AB=AC;②AD=AE;③BD=CE.请在以上三个等式中选择两个作为条件,另一个作为结论并进行证明.(写出已知、试说明及证明过程)
如图,点D、E在△ABC的边BC上,连接AD、AE.①AB=AC;②AD=AE;③BD=CE.请在以上三个等式中选择两个作为条件,另一个作为结论并进行证明.(写出已知、试说明及证明过程)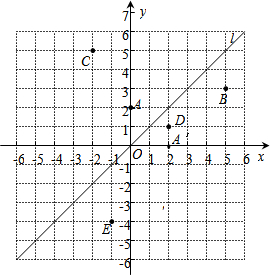 如图,在平面直角坐标系中,直线l的解析式是y=x.
如图,在平面直角坐标系中,直线l的解析式是y=x.
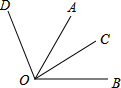 如图,∠AOB=60°,OC平分∠AOB,∠AOD=51°,求∠COD的余角的度数.
如图,∠AOB=60°,OC平分∠AOB,∠AOD=51°,求∠COD的余角的度数. 如图,在⊙O中,过弦AB的中点E作弦CD,且CE=2,DE=4,求弦AB的长.
如图,在⊙O中,过弦AB的中点E作弦CD,且CE=2,DE=4,求弦AB的长.