题目内容
9.若实数a,b是一直角三角形的两条边长,且满足b=$\sqrt{a-4}+\sqrt{4-a}+6$,则该三角形的第三条边长是2$\sqrt{5}$或2$\sqrt{13}$.分析 首先根据二次根式有意义的条件得出a,b的值,再利用勾股定理求出答案.
解答 解:∵实数a,b是一直角三角形的两条边长,且满足b=$\sqrt{a-4}+\sqrt{4-a}+6$,
∴a=4,b=6,
∴当a,b为直角边,则该三角形的第三条边长是:$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
当b为斜边,则该三角形的第三条边长是:$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$或2$\sqrt{13}$.
点评 此题主要考查了勾股定理以及二次根式有意义的条件,正确得出a,b的值是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4.关于x的不等式组$\left\{\begin{array}{l}{x-3>0}\\{x+a<2}\end{array}\right.$有2个整数解,则a的取值范围是( )
| A. | -4≤a<-3 | B. | -4<a≤-3 | C. | -5≤a<-4 | D. | -5<a≤-4 |
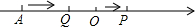 如图,在数轴上点A对应的数为-6,点P从原点O出发以每秒1个单位长度的速度向正方向运动,同时,点Q从点A出发以每秒2个单位长度的速度向正方向运动,则经过$\frac{12}{7}$或12秒钟,OQ=$\frac{3}{2}$OP.
如图,在数轴上点A对应的数为-6,点P从原点O出发以每秒1个单位长度的速度向正方向运动,同时,点Q从点A出发以每秒2个单位长度的速度向正方向运动,则经过$\frac{12}{7}$或12秒钟,OQ=$\frac{3}{2}$OP.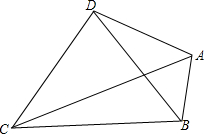 如图,四边形ABCD中,AC、BD为对角线,AC=10,BC=6,∠ADB=∠ABD=∠ACB=30°,那么线段CD的长为10$\sqrt{3}$-6.
如图,四边形ABCD中,AC、BD为对角线,AC=10,BC=6,∠ADB=∠ABD=∠ACB=30°,那么线段CD的长为10$\sqrt{3}$-6. 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BF⊥CD于点F,AB交CD于点E,求证:AD=BF-DF.
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BF⊥CD于点F,AB交CD于点E,求证:AD=BF-DF.