题目内容
18.已知y1与x成正比例关系,y2与x-1成反比例关系,且y=y1+y2,当x=0时,y=1;当x=3时,y=0,则y与x之间的函数表达式为y=$\frac{1}{6}$x-$\frac{1}{x-1}$.分析 先设y1=k1x,y2=$\frac{{k}_{2}}{x-1}$(k1≠0,k2≠0),代入等式y=y1+y2中,并将两点代入列方程组求出字母系数,再写出函数关系式即可.
解答 解:设y1=k1x,y2=$\frac{{k}_{2}}{x-1}$(k1≠0,k2≠0),
∴y=y1+y2=k1x+$\frac{{k}_{2}}{x-1}$,
把当x=0时,y=1;当x=3时,y=0分别代入得:$\left\{\begin{array}{l}{1=-{k}_{2}}\\{0=3{k}_{1}+\frac{{k}_{2}}{3-1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{6}}\\{{k}_{2}=-1}\end{array}\right.$,
∴y与x之间的函数表达式为:y=$\frac{1}{6}$x-$\frac{1}{x-1}$;
故答案为:y=$\frac{1}{6}$x-$\frac{1}{x-1}$.
点评 本题考查了利用待定系数法求正比例函数和反比例函数的解析式,是一种组合函数,与单独的正比例函数类似,都是将函数上的点代入列方程组进行求解.

练习册系列答案
相关题目
9. 如图,已知 l1∥l2∥l3,AB=3,DE=2,EF=4,则AC的长为( )
如图,已知 l1∥l2∥l3,AB=3,DE=2,EF=4,则AC的长为( )
 如图,已知 l1∥l2∥l3,AB=3,DE=2,EF=4,则AC的长为( )
如图,已知 l1∥l2∥l3,AB=3,DE=2,EF=4,则AC的长为( )| A. | 6 | B. | 9 | C. | 3 | D. | 4 |
7.小明沿着坡度为1:2的山坡向上走了100m,则他升高了( )
| A. | 20$\sqrt{5}$m | B. | 50m | C. | 50$\sqrt{3}$m | D. | 100m |

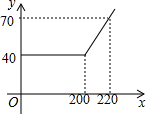 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.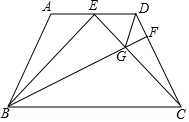 如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE
如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE