题目内容
3.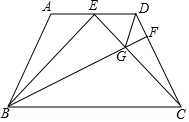 如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE
如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE(1)求证:BE=CE;
(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.
分析 (1)由等腰梯形ABCD中,AD∥BC,AB=DC,根据等腰梯形同一底上的两个角相等,可证得∠BAE=∠CDE,继而可证得△BAE≌△CDE,则可证得BE=CE;
(2)首先延长CD和BE的延长线交于H,易证得△BEG≌△CEH与△GED≌△HED,则可证得BG=DG+CD.
解答 解:∵等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,
∴∠BAE=∠CDE,AE=DE,
在△BAE与△CDE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠BAE=∠CDE}\\{AE=DE}\end{array}\right.$,
∴△BAE≌△CDE(SAS),
∴BE=CE;
(2)延长CD和BE的延长线交于H,
∵BF⊥CD,∠BEC=90°,
∴∠HEC=90°,
∴∠EBF+∠H=∠ECH+∠H=90°,
∴∠EBF=∠ECH,
在△BEG和△CEH中,
$\left\{\begin{array}{l}{∠EBF=∠ECH}\\{BE=CE}\\{∠BEC=∠CEH=90°}\end{array}\right.$,
∴△BEG≌△CEH(ASA),
∴EG=EH,BG=CH=DH+CD,
∵△BAE≌△CDE,
∴∠AEB=∠GED,
∠HED=∠AEB,
∴∠GED=∠HED,
在△GED和△HED中,
$\left\{\begin{array}{l}{EG=EH}\\{∠GED=∠HED}\\{ED=ED}\end{array}\right.$,
∴△GED≌△HED(SAS),
∴DG=DH,
∴BG=DG+CD
点评 此题考查了等腰梯形的性质、等腰三角形的性质以及全等三角形的判定与性质.此题难度较大,解题的关键是准确作出辅助线,利用数形结合思想求解.

练习册系列答案
相关题目
13.下列各式计算正确的是( )
| A. | 2a+3b=5ab | B. | 3a2+2a3=5a5 | C. | 6ab-ab=5ab | D. | 5+a=5a |
8.如图都是有几个黑色和白色的正方形按一定规律组成,图1中有2个黑色正方形,图2中有5个黑色正方形,图3中有8个黑色正方形,图4中有11个黑色正方形,…,按此规律,图n中黑色正方形的个数是( )
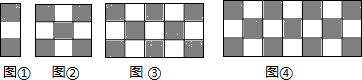

| A. | 3n-1 | B. | 3n+1 | C. | 4n-1 | D. | 4n+1 |
12. 某中学举行“班班有歌声”活动,比赛时聘请了10位老师和10位学生担任评委,其中甲班的得分情况如下统计图(表)所示.
某中学举行“班班有歌声”活动,比赛时聘请了10位老师和10位学生担任评委,其中甲班的得分情况如下统计图(表)所示.
老师评委计分统计表:
请完成下列各题:
(1)学生评委计分的众数是95分;中位数是95分;
(2)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,且按老师、学生各占60%,40%的方法计算各班最后得分,已知甲班最后得分为94.4分.
①求学生评委的平均分;
②求教师评委的平均分;
③直接写出统计表中x的值.
 某中学举行“班班有歌声”活动,比赛时聘请了10位老师和10位学生担任评委,其中甲班的得分情况如下统计图(表)所示.
某中学举行“班班有歌声”活动,比赛时聘请了10位老师和10位学生担任评委,其中甲班的得分情况如下统计图(表)所示.老师评委计分统计表:
| 评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
(1)学生评委计分的众数是95分;中位数是95分;
(2)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,且按老师、学生各占60%,40%的方法计算各班最后得分,已知甲班最后得分为94.4分.
①求学生评委的平均分;
②求教师评委的平均分;
③直接写出统计表中x的值.
13.下列运算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | -$\sqrt{25}$=-5 | C. | -|-5|=5 | D. | -52=25 |
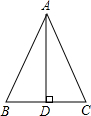 如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为4.
如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为4.