题目内容
6.(1)请用“>”、“<”、“=”填空:①32+22>2×3×2;
②($\sqrt{3}$)2+($\sqrt{2}$)2>2×$\sqrt{3}$×$\sqrt{2}$;
③52+52=2×5×5;
④(-2)2+(-2)2=2×(-2)×(-2)
(2)观察以上各式,请猜想a2+b2与2ab的大小;
(3)请你借助完全平方公式证明你的猜想.
分析 (1)①求出式子的结果,即可得出答案;
②求出式子的结果,即可得出答案;
③求出式子的结果,即可得出答案;
④求出式子的结果,即可得出答案;
(2)根据求出的结果得出即可;
(3)根据完全平方公式求出即可.
解答 解:(1)①∵32+22=13,2×3×2=12,
∴32+22>2×3×2,
故答案为:>;
②∵($\sqrt{3}$)2+($\sqrt{2}$)2=5,2×$\sqrt{3}$×$\sqrt{2}$=2$\sqrt{6}$=$\sqrt{24}$,
∴($\sqrt{3}$)2+($\sqrt{2}$)2>2×$\sqrt{3}$×$\sqrt{2}$,
故答案为:>;
③∵52+52=50,2×5×5=50,
∴52+52=2×5×5,
故答案为:=;
④∵(-2)2+(-2)2=8,2×(-2)×(-2)=8,
∴(-2)2+(-2)2=2×(-2)×(-2),
故答案为:=;
(2)a2+b2≥2ab;
(3)证明:∵(a+b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab.
点评 本题考查了完全平方公式的应用,能根据求出的结果得出规律是解此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
16.函数y=-x2-2x+3的图象由y=-x2怎样平移得到( )
| A. | 向右1个单位,向上4个单位 | B. | 向左1个单位,向下4个单位 | ||
| C. | 向左1个单位,向上4个单位 | D. | 向右1个单位,向下4个单位 |
 如图,BC⊥AC于点C,CD⊥AB于点D,BE∥CD. 求证:∠EBC=∠A.
如图,BC⊥AC于点C,CD⊥AB于点D,BE∥CD. 求证:∠EBC=∠A. 如图,已知AB=CD,不添加新的线段和字母,要使△AOB≌△COD,需添加的一个条件是∠A=∠C或∠B=∠D或AB∥CD.
如图,已知AB=CD,不添加新的线段和字母,要使△AOB≌△COD,需添加的一个条件是∠A=∠C或∠B=∠D或AB∥CD.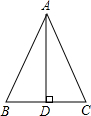 如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为4.
如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为4.