题目内容
已知△ABC中,边BC的长与BC边上的高的和为20.
(1)写出△ABC的面积y与BC的长x之间的函数关系式,当△ABC的面积为48,且BC边上的高大于BC时,求出BC的长;
(2)当BC多长时,△ABC的面积最大?最大面积是多少?
(3)当△ABC的面积不小于48时,请直接写出BC长的取值范围.
(1)写出△ABC的面积y与BC的长x之间的函数关系式,当△ABC的面积为48,且BC边上的高大于BC时,求出BC的长;
(2)当BC多长时,△ABC的面积最大?最大面积是多少?
(3)当△ABC的面积不小于48时,请直接写出BC长的取值范围.
考点:二次函数的应用
专题:
分析:(1)先表示出三角形的高,由三角形的面积公式就可以表示出y与x之间的数量关系,当y=48时求出x的值即可;
(2)将(1)的解析式转化为顶点式就可以求出结论;
(3)根据解析式就可以求出函数的开口方向,当48=-0.5x2+10x求出x的值,由抛物线的性质就可以求出结论.
(2)将(1)的解析式转化为顶点式就可以求出结论;
(3)根据解析式就可以求出函数的开口方向,当48=-0.5x2+10x求出x的值,由抛物线的性质就可以求出结论.
解答:解:(1)由题意,得
y=
,
∴y=-0.5x2+10x,
当y=48时,48=-0.5x2+10x,
解得:x1=12,x2=8.
当x=12时,高为8,当x=8时,高为12.
∵BC边上的高大于BC,
∴BC=8.
答:y与BC的长x之间的函数关系式为y=-0.5x2+10x,当△ABC的面积为48,且BC边上的高大于BC时,BC的长为8;
(2)∵y=-0.5x2+10x,
∴y=-0.5(x-10)2+50,
∴a=-0.5<0,
∴x=10时,y最大=50.
答:当BC=10时,△ABC的面积最大,最大面积是50;
(3)由题意,得
-0.5x2+10x=48时,
x1=12,x2=8.
∵a=-0.5<0,
∴抛物线的开口向下,由函数图象可以得出当y≥48时,
∴8≤BC≤12.
y=
| x(20-x) |
| 2 |
∴y=-0.5x2+10x,
当y=48时,48=-0.5x2+10x,
解得:x1=12,x2=8.
当x=12时,高为8,当x=8时,高为12.
∵BC边上的高大于BC,
∴BC=8.
答:y与BC的长x之间的函数关系式为y=-0.5x2+10x,当△ABC的面积为48,且BC边上的高大于BC时,BC的长为8;
(2)∵y=-0.5x2+10x,
∴y=-0.5(x-10)2+50,
∴a=-0.5<0,
∴x=10时,y最大=50.
答:当BC=10时,△ABC的面积最大,最大面积是50;
(3)由题意,得
-0.5x2+10x=48时,
x1=12,x2=8.
∵a=-0.5<0,
∴抛物线的开口向下,由函数图象可以得出当y≥48时,
∴8≤BC≤12.
点评:本题考查了三角形的面积公式的运用,一元二次方程的解法的运用,二次函数的顶点式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
 如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )
如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )| A、90° | B、100° |
| C、110° | D、120° |
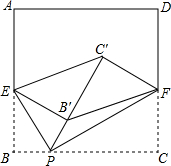 如图,已知,正方形纸片ABCD的边长为4,点P在BC边上,BP=1,点E在AB边上,且∠BPE=60°,沿PE翻折△EBP得到△EB′P. F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点Cˊ落在射线PBˊ上.
如图,已知,正方形纸片ABCD的边长为4,点P在BC边上,BP=1,点E在AB边上,且∠BPE=60°,沿PE翻折△EBP得到△EB′P. F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点Cˊ落在射线PBˊ上.