题目内容
 如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )
如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )| A、90° | B、100° |
| C、110° | D、120° |
考点:切线的性质
专题:
分析:根据切线性质得出∠OAP=∠OBP=90°,∠APO=∠BPO,求出∠AOP=∠BOP,解直角三角形求出∠AOP和∠BOP,即可得出答案.
解答:解:∵PA,PB是⊙O的两条切线,切点是A,B,
∴∠OAP=∠OBP=90°,∠APO=∠BPO,
∴∠AOP=∠BOP,
∵cos∠AOP=
=
=
,
∴∠AOP=60°,
∴∠BOP=60°,
∴∠AOB=60°+60°=120°,
故选D.
∴∠OAP=∠OBP=90°,∠APO=∠BPO,
∴∠AOP=∠BOP,
∵cos∠AOP=
| OA |
| OP |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠AOP=60°,
∴∠BOP=60°,
∴∠AOB=60°+60°=120°,
故选D.
点评:本题考查了切线的性质,解直角三角形,三角形的内角和定理的应用,解此题的关键是求出∠AOP和∠BOP,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
 如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是( )
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是( )A、4π+4
| ||
| B、4π | ||
C、2π+4
| ||
| D、2π |
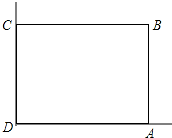 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=13cm,BC=12cm,求CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=13cm,BC=12cm,求CD的长.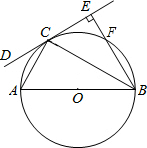 如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.
如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.