题目内容
1. 如图所示,在△ABC中,AD为∠BAC的角平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm.AC=8cm,求DE的长.(只能用≌)
如图所示,在△ABC中,AD为∠BAC的角平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm.AC=8cm,求DE的长.(只能用≌)
分析 利用“角角边”证明△ADE和△ADF全等,根据全等三角形对应边相等可得DE=DF,然后根据S△ABC=S△ABD+S△ACD列方程求解即可.
解答 解:∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△ADE和△ADF中,$\left\{\begin{array}{l}{∠BAD=∠CAD}\\{∠AED=∠AFD=90°}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADF(AAS),
∴DE=DF,
由S△ABC=S△ABD+S△ACD得,$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=28,
∵AB=20cm.AC=8cm,
∴$\frac{1}{2}$×20•DE+$\frac{1}{2}$×8•DE=28,
解得DE=2cm.
点评 本题考查了全等三角形的判定与性质,三角形的面积,本题虽然利用角平分线上的点到角的两边距离相等的性质更简便,要注意题目的要求.

练习册系列答案
相关题目
12.某校初三(7)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如表:
(1)求a、b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,用树状图或列表法求所抽取的两名学生恰好是两名女生的概率.
| 自选项目 | 人 数 | 频 率 |
| 立定跳远 | 9 | 0.18 |
| 三级蛙跳 | 12 | a |
| 一分钟跳绳 | 8 | 0.16 |
| 投掷实心球 | b | 0.32 |
| 推铅球 | 5 | 0.10 |
| 合 计 | 50 | 1 |
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,用树状图或列表法求所抽取的两名学生恰好是两名女生的概率.
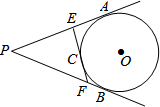 如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为10cm.
如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为10cm. 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点,点P是AC上的一动点,过点P作PD∥y轴,与抛物线交于点D.
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点,点P是AC上的一动点,过点P作PD∥y轴,与抛物线交于点D. 如图,已知直线L1∥L2,直线L3和直线L1、L2交于点C和D,在C、D之间有一点P.
如图,已知直线L1∥L2,直线L3和直线L1、L2交于点C和D,在C、D之间有一点P.